题目
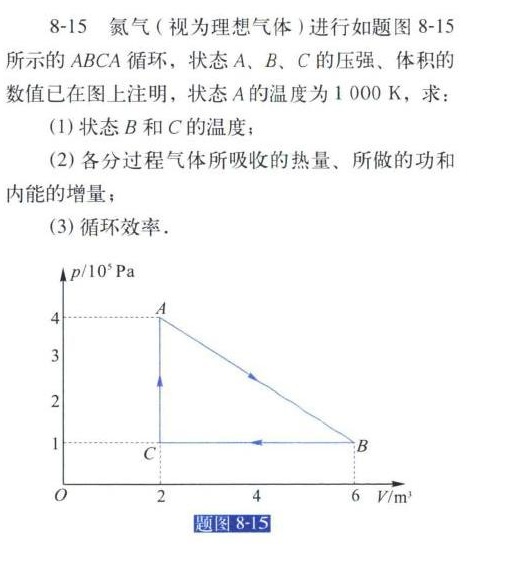
8-15 氮气(视为理想气体)进行如题图 8-15-|||-所示的ABCA循环,状态A、B、C的压强、体积的-|||-数值已在图上注明,状态A的温度为1000 K,求:-|||-(1)状态B和C的温度;-|||-(2)各分过程气体所吸收的热量、所做的功和-|||-内能的增量;-|||-(3)循环效率.-|||-4 p/10^5Pa-|||-4 A-|||-3-|||-2-|||-1 C B-|||-2 4 6 V/m^3
题目解答
答案
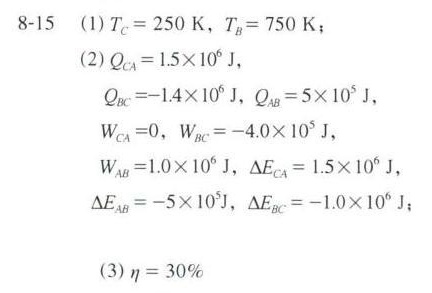
解析
步骤 1:确定状态B和C的温度
根据理想气体状态方程 $PV=nRT$,其中 $P$ 是压强,$V$ 是体积,$n$ 是摩尔数,$R$ 是理想气体常数,$T$ 是温度。由于摩尔数 $n$ 和理想气体常数 $R$ 在整个过程中保持不变,我们可以使用 $PV/T$ 的比值来确定温度。已知状态A的温度为1000K,压强为4×10^5Pa,体积为2m^3。状态B的压强为1×10^5Pa,体积为6m^3。状态C的压强为1×10^5Pa,体积为2m^3。
步骤 2:计算状态B的温度
根据理想气体状态方程,$P_AV_A/T_A = P_BV_B/T_B$,代入已知数值,可以求得状态B的温度。
步骤 3:计算状态C的温度
根据理想气体状态方程,$P_AV_A/T_A = P_CV_C/T_C$,代入已知数值,可以求得状态C的温度。
步骤 4:计算各分过程的热量、功和内能增量
根据热力学第一定律,$Q = \Delta U + W$,其中 $Q$ 是热量,$\Delta U$ 是内能增量,$W$ 是功。对于理想气体,内能增量 $\Delta U = nC_v\Delta T$,其中 $C_v$ 是定容摩尔热容。对于等压过程,$W = P\Delta V$;对于等容过程,$W = 0$。
步骤 5:计算循环效率
循环效率 $n = W_{net}/Q_{in}$,其中 $W_{net}$ 是净功,$Q_{in}$ 是输入的热量。
根据理想气体状态方程 $PV=nRT$,其中 $P$ 是压强,$V$ 是体积,$n$ 是摩尔数,$R$ 是理想气体常数,$T$ 是温度。由于摩尔数 $n$ 和理想气体常数 $R$ 在整个过程中保持不变,我们可以使用 $PV/T$ 的比值来确定温度。已知状态A的温度为1000K,压强为4×10^5Pa,体积为2m^3。状态B的压强为1×10^5Pa,体积为6m^3。状态C的压强为1×10^5Pa,体积为2m^3。
步骤 2:计算状态B的温度
根据理想气体状态方程,$P_AV_A/T_A = P_BV_B/T_B$,代入已知数值,可以求得状态B的温度。
步骤 3:计算状态C的温度
根据理想气体状态方程,$P_AV_A/T_A = P_CV_C/T_C$,代入已知数值,可以求得状态C的温度。
步骤 4:计算各分过程的热量、功和内能增量
根据热力学第一定律,$Q = \Delta U + W$,其中 $Q$ 是热量,$\Delta U$ 是内能增量,$W$ 是功。对于理想气体,内能增量 $\Delta U = nC_v\Delta T$,其中 $C_v$ 是定容摩尔热容。对于等压过程,$W = P\Delta V$;对于等容过程,$W = 0$。
步骤 5:计算循环效率
循环效率 $n = W_{net}/Q_{in}$,其中 $W_{net}$ 是净功,$Q_{in}$ 是输入的热量。