题目
计算定积分 (int )_(-1)^1(dfrac (x)(sqrt {5-4x)}+dfrac (xcos x)(1+{x)^4})dx. (8分)-|||-__
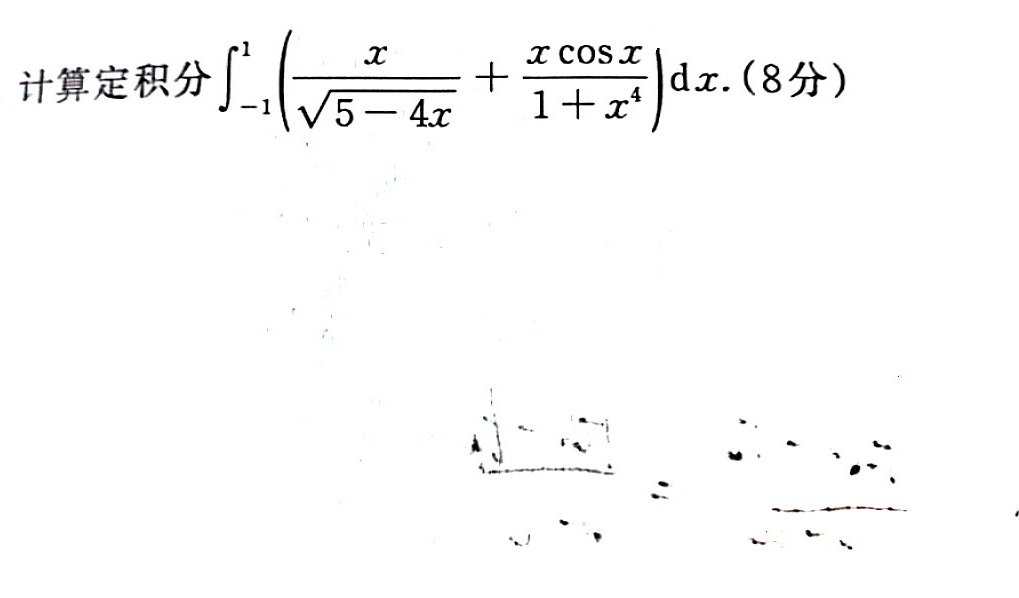
题目解答
答案

解析
考查要点:本题主要考查定积分的计算,特别是利用奇偶函数的对称性简化积分,以及通过变量代换法处理复杂积分。
解题核心思路:
- 拆分积分:将积分拆分为两个部分,分别处理。
- 奇偶性判断:第二部分被积函数为奇函数,在对称区间积分结果为0。
- 变量代换:对第一部分进行变量代换,转化为容易计算的积分形式。
破题关键点:
- 识别奇函数:第二部分被积函数为奇函数,直接得出积分值为0。
- 变量代换简化计算:通过代换$u=5-4x$,将第一部分积分转化为关于$u$的简单积分。
第一部分积分 $\int_{-1}^{1} \dfrac{x}{\sqrt{5-4x}} dx$
变量代换
令 $u = 5 - 4x$,则 $du = -4dx$,即 $dx = -\dfrac{du}{4}$。当$x=-1$时,$u=9$;当$x=1$时,$u=1$。此时积分变为:
$\begin{aligned}\int_{9}^{1} \dfrac{\dfrac{5-u}{4}}{\sqrt{u}} \cdot \left(-\dfrac{du}{4}\right) &= \dfrac{1}{16} \int_{1}^{9} \dfrac{5-u}{\sqrt{u}} du \\&= \dfrac{1}{16} \int_{1}^{9} \left(5u^{-1/2} - u^{1/2}\right) du\end{aligned}$
分项积分
分别计算两部分:
- $\int 5u^{-1/2} du = 10u^{1/2}$,代入上下限得 $10(3 - 1) = 20$;
- $\int u^{1/2} du = \dfrac{2}{3}u^{3/2}$,代入上下限得 $\dfrac{2}{3}(27 - 1) = \dfrac{52}{3}$。
合并结果
$\dfrac{1}{16} \left(20 - \dfrac{52}{3}\right) = \dfrac{1}{16} \cdot \dfrac{8}{3} = \dfrac{1}{6}$
第二部分积分 $\int_{-1}^{1} \dfrac{x \cos x}{1+x^4} dx$
奇偶性判断
被积函数为奇函数($f(-x) = -f(x)$),在对称区间$[-1,1]$上的积分为0。