题目
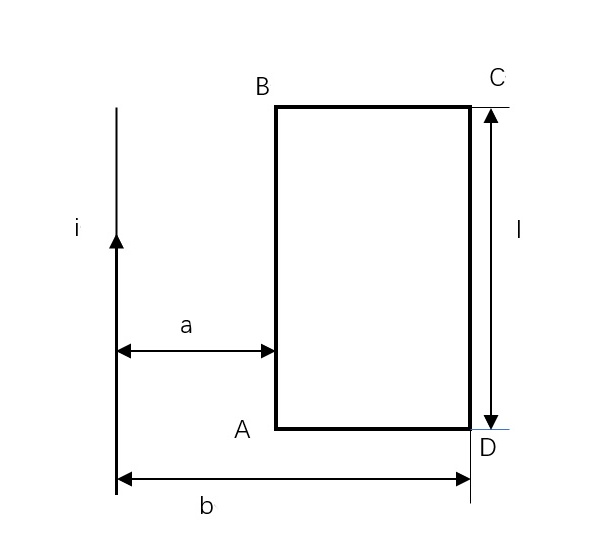
如图所示，长直导线和矩形线圈共面， AB边到导线的距离为 a ，CD 边到导线的距离为 b，AB、CD 边长为 l，若导线中的电流 i 在1s内均匀地从1A降到零，则线圈 ABCD 中的感应电动势的大小和方向？B C-|||-4-|||-a-|||-A-|||-D-|||-→-|||-b
如图所示，长直导线和矩形线圈共面， AB边到导线的距离为 a ，CD 边到导线的距离为 b，AB、CD 边长为 l，若导线中的电流 i 在1s内均匀地从1A降到零，则线圈 ABCD 中的感应电动势的大小和方向？
题目解答
答案
设AD上某点到导线距离为x.
在线圈上取微元dx，根据安培环路定理，此处的磁感应强度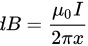
由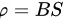
,则这一段面积内的磁通量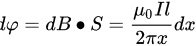
则根据积分知识，线圈的磁通量为
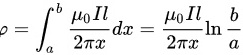
导线中的电流 i 在1s内均匀地从1A降到零，该过程中磁通量的变化为
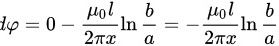
由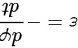
得，产生的感应电动势为
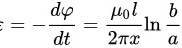
感应电动势的方向为顺时针方向。
解析
步骤 1：确定磁感应强度
根据安培环路定理，长直导线在距离导线x处的磁感应强度为$B=\dfrac{{\mu}_0I}{2\pi x}$，其中${\mu}_0$是真空磁导率，I是导线中的电流，x是到导线的距离。
步骤 2：计算磁通量
在线圈上取微元dx，这一段面积内的磁通量为$\varphi =dB\cdot S=\dfrac{{\mu}_0IL}{2\pi x}dx$。对整个线圈进行积分，得到线圈的磁通量为$\rho ={\int }_{a}^{b}\dfrac{{\mu}_0IL}{2\pi x}dx=\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}$。
步骤 3：计算感应电动势
导线中的电流 i 在1s内均匀地从1A降到零，该过程中磁通量的变化为$\Delta\varphi =0-\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}=-\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}$。根据法拉第电磁感应定律，感应电动势为$e=-\dfrac{d\varphi}{dt}=\dfrac{{\mu}_0L}{2\pi}\ln\frac{b}{a}$。感应电动势的方向由楞次定律确定，为顺时针方向。
根据安培环路定理，长直导线在距离导线x处的磁感应强度为$B=\dfrac{{\mu}_0I}{2\pi x}$，其中${\mu}_0$是真空磁导率，I是导线中的电流，x是到导线的距离。
步骤 2：计算磁通量
在线圈上取微元dx，这一段面积内的磁通量为$\varphi =dB\cdot S=\dfrac{{\mu}_0IL}{2\pi x}dx$。对整个线圈进行积分，得到线圈的磁通量为$\rho ={\int }_{a}^{b}\dfrac{{\mu}_0IL}{2\pi x}dx=\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}$。
步骤 3：计算感应电动势
导线中的电流 i 在1s内均匀地从1A降到零，该过程中磁通量的变化为$\Delta\varphi =0-\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}=-\dfrac{{\mu}_0IL}{2\pi}\ln\frac{b}{a}$。根据法拉第电磁感应定律，感应电动势为$e=-\dfrac{d\varphi}{dt}=\dfrac{{\mu}_0L}{2\pi}\ln\frac{b}{a}$。感应电动势的方向由楞次定律确定，为顺时针方向。