题目
如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α．现把一质量为m 的滑块B 放在三棱柱的光滑斜面上．试求： B.-|||-A-|||-m-|||-aA-|||-m` (1)三棱柱相对于地面的加速度； (2) 滑块相对于地面的加速度； (3) 滑块与三棱柱之间的正压力．
如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α．现把一质量为m 的滑块B 放在三棱柱的光滑斜面上．试求：
(1)三棱柱相对于地面的加速度；
(2) 滑块相对于地面的加速度；
(3) 滑块与三棱柱之间的正压力．
题目解答
答案
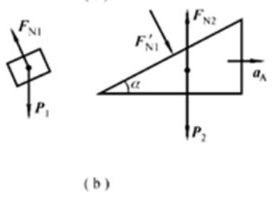
取地面为参考系,以滑块B 和三棱柱A 为研究对象,分别作示力图,如图(b)所示．
B 受重力
、A 施加的支持力
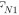；A 受重力
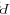、B 施加的压力
、地面支持力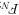
．A 的运动方向为Ox 轴的正向,Oy轴的正向垂直地面向上．设
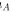为A 对地的加速度,
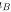为B 对的地加速度．由牛顿定律得
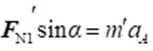(1)
(2)
(3)
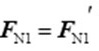(4)
设B 相对A 的加速度为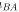
,则由题意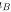 、、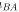 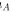三者的矢量关系如图(c)所示．
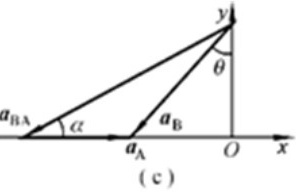
据此可得
(5)
(6)
解上述方程组可得三棱柱对地面的加速度为
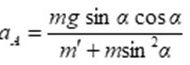
滑块相对地面的加速度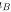 在x、y 轴上的分量分别为
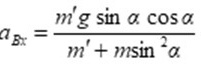
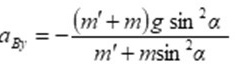
则滑块相对地面的加速度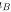 的大小为
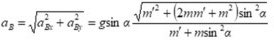
其方向与y轴负向的夹角为
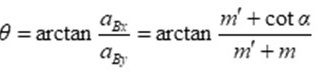
A 与B 之间的正压力
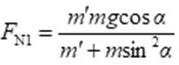
解析
步骤 1：确定受力分析
取地面为参考系，以滑块B 和三棱柱A 为研究对象，分别作示力图，如图(b)所示。B 受重力 、A 施加的支持力N1 ；A 受重力、B 施加的压力N1、地面支持力Nd 。A 的运动方向为Ox 轴的正向，Oy轴的正向垂直地面向上。设 为A 对地的加速度，为B 对的地加速度。
步骤 2：列出牛顿定律方程
由牛顿定律得
${F}_{N1}\sin \alpha =m'{a}_{d}$ (1)
$-{F}_{N1}\sin \alpha =m{a}_{Bx}$ (2)
${F}_{N1}\cos \alpha -mg=m{a}_{By}$ (3)
${F}_{Nd}=m'g+{F}_{N1}\cos \alpha $ (4)
步骤 3：确定相对运动关系
设B 相对A 的加速度为BA ，则由题意 、BA、 三者的矢量关系如图(c)所示。据此可得
${a}_{Bx}={a}_{A}-{a}_{BA}\cos \alpha $ (5)
${a}_{By}=-{a}_{BA}\sin \alpha $ (6)
步骤 4：解方程组
解上述方程组可得三棱柱对地面的加速度为
${a}_{d}=\dfrac {mg\sin \alpha \cos \alpha }{m'+m{\sin }^{2}\alpha }$
滑块相对地面的加速度 在x、y 轴上的分量分别为
${a}_{Bx}=\dfrac {m'g\sin \alpha \cos \alpha }{m'+m{\sin }^{2}\alpha }$
${a}_{By}=-\dfrac {(m'+m)g{\sin }^{2}a}{m'+m{\sin }^{2}a}$
则滑块相对地面的加速度 的大小为
${a}_{B}=\sqrt {{{a}_{Bx}}^{2}+{{a}_{By}}^{2}=g\sin \alpha \dfrac {\sqrt {{m}^{2}+(2mm+{m}^{2}){\sin }^{2}\alpha }}{{m}^{2}+m{\sin }^{2}\alpha }}$
其方向与y轴负向的夹角为
$\theta =\arctan \dfrac {{a}_{Bx}}{{a}_{By}}=\arctan \dfrac {m'+\cot \alpha }{m'+m}$
A 与B 之间的正压力
${F}_{N}=\dfrac {m'mg\cos \alpha }{m'+m{\sin }^{2}\alpha }$
取地面为参考系，以滑块B 和三棱柱A 为研究对象，分别作示力图，如图(b)所示。B 受重力 、A 施加的支持力N1 ；A 受重力、B 施加的压力N1、地面支持力Nd 。A 的运动方向为Ox 轴的正向，Oy轴的正向垂直地面向上。设 为A 对地的加速度，为B 对的地加速度。
步骤 2：列出牛顿定律方程
由牛顿定律得
${F}_{N1}\sin \alpha =m'{a}_{d}$ (1)
$-{F}_{N1}\sin \alpha =m{a}_{Bx}$ (2)
${F}_{N1}\cos \alpha -mg=m{a}_{By}$ (3)
${F}_{Nd}=m'g+{F}_{N1}\cos \alpha $ (4)
步骤 3：确定相对运动关系
设B 相对A 的加速度为BA ，则由题意 、BA、 三者的矢量关系如图(c)所示。据此可得
${a}_{Bx}={a}_{A}-{a}_{BA}\cos \alpha $ (5)
${a}_{By}=-{a}_{BA}\sin \alpha $ (6)
步骤 4：解方程组
解上述方程组可得三棱柱对地面的加速度为
${a}_{d}=\dfrac {mg\sin \alpha \cos \alpha }{m'+m{\sin }^{2}\alpha }$
滑块相对地面的加速度 在x、y 轴上的分量分别为
${a}_{Bx}=\dfrac {m'g\sin \alpha \cos \alpha }{m'+m{\sin }^{2}\alpha }$
${a}_{By}=-\dfrac {(m'+m)g{\sin }^{2}a}{m'+m{\sin }^{2}a}$
则滑块相对地面的加速度 的大小为
${a}_{B}=\sqrt {{{a}_{Bx}}^{2}+{{a}_{By}}^{2}=g\sin \alpha \dfrac {\sqrt {{m}^{2}+(2mm+{m}^{2}){\sin }^{2}\alpha }}{{m}^{2}+m{\sin }^{2}\alpha }}$
其方向与y轴负向的夹角为
$\theta =\arctan \dfrac {{a}_{Bx}}{{a}_{By}}=\arctan \dfrac {m'+\cot \alpha }{m'+m}$
A 与B 之间的正压力
${F}_{N}=\dfrac {m'mg\cos \alpha }{m'+m{\sin }^{2}\alpha }$