某工场每天生产x后袖珍收音机,总成本为:(x)=dfrac (1)(4)(x)^2+x+100-|||-__(元),该种收音机独家经营,市场需求规律为x=75-3p,其中p为单价,问每天生产多少台时获利最大?此时每台收音机价格如何?
某工场每天生产x后袖珍收音机,总成本为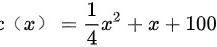 (元),该种收音机独家经营,市场需求规律为x=75-3p,其中p为单价,问每天生产多少台时获利最大?此时每台收音机价格如何?
(元),该种收音机独家经营,市场需求规律为x=75-3p,其中p为单价,问每天生产多少台时获利最大?此时每台收音机价格如何?
题目解答
答案
步骤一:求出总收益函数$R(x)$
已知市场需求规律为$x = 75 - 3p$,解出$p$关于$x$的表达式:$3p = 75 - x$,即$p=\frac{75 - x}{3}=25 - \frac{1}{3}x$。 总收益$R(x)$等于单价$p$乘以产量$x$,将$p = 25 - \frac{1}{3}x$代入可得:$R(x)=px=(25 - \frac{1}{3}x)x=25x - \frac{1}{3}x^{2}$。
步骤二:求出利润函数$L(x)$
利润$L(x)$等于总收益$R(x)$减去总成本$C(x)$,已知$C(x)=\frac{1}{4}x^{2}+x + 100$,则:$L(x)=R(x)-C(x)=25x - \frac{1}{3}x^{2}-(\frac{1}{4}x^{2}+x + 100)=25x - \frac{1}{3}x^{2}-\frac{1}{4}x^{2}-x - 100=24x - \frac{7}{12}x^{2}-100$。
步骤三:求利润函数$L(x)$的最大值
对$L(x)=24x - \frac{7}{12}x^{2}-100$求导,根据求导公式$(X^n)^\prime=nX^{n - 1}$可得:$L^\prime(x)=(24x - \frac{7}{12}x^{2}-100)^\prime=24 - \frac{7}{6}x$。 令$L^\prime(x)=0$,即$24 - \frac{7}{6}x = 0$,解这个方程:$\frac{7}{6}x = 24$,$x = \frac{144}{7}\approx 20.57$。 再对$L^\prime(x)$求导,可得$L^{\prime\prime}(x)=-\frac{7}{6}\lt 0$,这说明函数$L(x)$在$x = \frac{144}{7}$处取得极大值,由于函数只有一个极值点,所以该极大值就是最大值。 因为$x$表示生产的台数,应当取整数,分别计算$x = 20$和$x = 21$时的利润:
- 当$x = 20$时,$L(20)=24\times20 - \frac{7}{12}\times20^{2}-100=480 - \frac{7}{12}\times400 - 100=480 - \frac{700}{3} - 100=\frac{1440 - 700 - 300}{3}=\frac{440}{3}\approx 146.67$(元)。
- 当$x = 21$时,$L(21)=24\times21 - \frac{7}{12}\times21^{2}-100=504 - \frac{7}{12}\times441 - 100=504 - \frac{3087}{12} - 100=\frac{6048 - 3087 - 1200}{12}=\frac{1761}{12}=146.75$(元)。 比较可得$x = 21$时利润更大,所以每天生产$21$台时获利最大。
步骤四:求出此时每台收音机的价格
将$x = 21$代入$p = 25 - \frac{1}{3}x$,可得:$p = 25 - \frac{1}{3}\times21=25 - 7 = 18$(元)。
综上,每天生产$21$台时获利最大,此时每台收音机价格为$18$元。