题目
当x→0时,变量 dfrac (1)({x)^2}sin dfrac (1)(x) 是-|||-__当x→0时,变量 dfrac (1)({x)^2}sin dfrac (1)(x) 是-|||-__


题目解答
答案
解析:
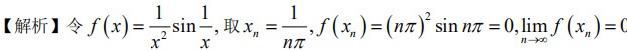
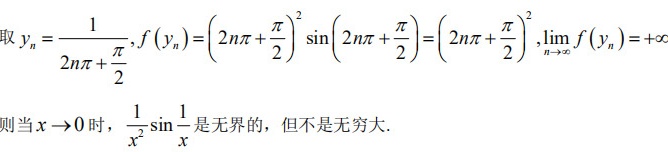
解析
考查要点:本题主要考查函数在极限过程中的有界性、无界性、无穷小和无穷大的判断,需要结合函数的具体形式分析其极限行为。
解题核心思路:
- 分析函数结构:函数由$\dfrac{1}{x^2}$和$\sin \dfrac{1}{x}$组成,前者在$x \to 0$时趋向无穷大,后者在$-1$到$1$之间振荡。
- 构造特殊序列:通过选取不同的$x$序列,观察函数值的变化趋势,判断是否存在无界性或极限存在性。
- 综合结论:若函数在某些序列下趋向无穷大,而在另一些序列下趋向有限值,则函数无界但极限不存在,从而排除其他选项。
破题关键点:
- 无界性:通过选取$x_n = \dfrac{1}{2n\pi + \dfrac{\pi}{2}}$,使$\sin \dfrac{1}{x_n} = 1$,此时$f(x_n) \to +\infty$,说明函数无界。
- 极限不存在:通过选取$x_n = \dfrac{1}{n\pi}$,使$f(x_n) = 0$,说明函数值在不同路径下趋于不同结果,极限不存在。
步骤1:分析函数结构
函数$f(x) = \dfrac{1}{x^2} \sin \dfrac{1}{x}$由两部分组成:
- $\dfrac{1}{x^2}$在$x \to 0$时趋向无穷大。
- $\sin \dfrac{1}{x}$在$-1$到$1$之间振荡,且振荡频率随$x \to 0$加快。
步骤2:构造特殊序列验证无界性
取序列$x_n = \dfrac{1}{2n\pi + \dfrac{\pi}{2}}$,此时:
$\sin \dfrac{1}{x_n} = \sin \left(2n\pi + \dfrac{\pi}{2}\right) = 1$
代入$f(x_n)$得:
$f(x_n) = \left(2n\pi + \dfrac{\pi}{2}\right)^2 \cdot 1 \to +\infty \quad (n \to \infty)$
说明函数在$x \to 0$时无界。
步骤3:验证极限不存在
取序列$x_n = \dfrac{1}{n\pi}$,此时:
$\sin \dfrac{1}{x_n} = \sin(n\pi) = 0$
代入$f(x_n)$得:
$f(x_n) = \dfrac{1}{x_n^2} \cdot 0 = 0 \quad \Rightarrow \quad \lim_{n \to \infty} f(x_n) = 0$
结合步骤2的结果,函数在不同路径下趋于不同极限,说明$x \to 0$时$f(x)$极限不存在,因此既不是无穷大也不是无穷小。