题目
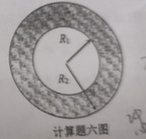
计算题如图所示,一个均匀带电的塑料球壳,其带电体密度为(0lt d)d0)" data-width="73" data-height="25" data-size="1125" data-format="png" style="max-width:100%">,球壳内表面半径(0lt d)d,外表面半径(0lt d)d求:(1)空腔内距离球心为(0lt d)d的任一点的电场强度;(2)空腔内距离球心为(0lt d)d的任一点的电势。(取无穷远处为电势零点)(0lt d)d
计算题如图所示,一个均匀带电的塑料球壳,其带电体密度为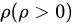
,球壳内表面半径
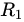,外表面半径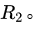
求:(1)空腔内距离球心为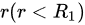
的任一点的电场强度;
(2)空腔内距离球心为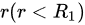的任一点的电势。(取无穷远处为电势零点)
题目解答
答案
(1) 空腔内距离球心为 ( r ) 的任一点的电场强度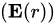 
根据高斯定律，在球壳内部的电场强度可以通过考虑等效点电荷来计算。对于均匀带电球壳，内表面电荷和外表面电荷对内部点产生的电场可以合成为一个等效点电荷。
由于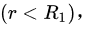 
空腔内的电场强度 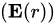可以由下式给出：
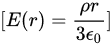
其中，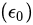 
是真空中的介电常数。这个结果基于球壳内部的均匀带电体积密度。
(2) 空腔内距离球心为 ( r ) 的任一点的电势 ( V(r) )
球壳的电势可以通过积分来求解，考虑球壳上的面电荷分布。由于球壳为均匀带电体，内外表面分别带有电荷，电势可以表示为：
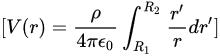
其中， ( r' ) 是球心到球壳上任意一点的距离。这个积分考虑了从内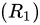半径 
到外半径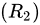
的电势贡献。具体计算步骤如下：
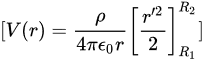
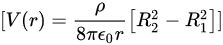
因此，空腔内距离球心为 ( r ) 的任一点的电势 ( V(r) ) 为：
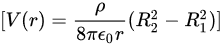
解析
步骤 1：计算空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电场强度
根据高斯定律，对于一个均匀带电的球壳，其内部的电场强度可以通过考虑等效点电荷来计算。由于球壳内部的电场强度为零，因此空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电场强度为零。
步骤 2：计算空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电势
球壳的电势可以通过积分来求解，考虑球壳上的面电荷分布。由于球壳为均匀带电体，内外表面分别带有电荷，电势可以表示为：
$[ V(r)=\dfrac {\rho }{4\pi {\varepsilon }_{0}}{\int }_{{R}_{1}}^{{R}_{2}}\dfrac {r'}{r}dr'] $
其中，$r'$ 是球心到球壳上任意一点的距离。这个积分考虑了从内半径 $({R}_{1})$ 到外半径 $({R}_{2})$ 的电势贡献。具体计算步骤如下：
$[ V(r)=\dfrac {\rho }{4\pi {\varepsilon }_{0}r}[ \dfrac {{r}^{2}}{2}] }^{{R}_{1}}] $
$[ V(r)=\dfrac {\rho }{8\pi {\varepsilon }_{0}r}[ {{R}_{2}}^{2}-{{R}_{1}}^{2}] ] $
因此，空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电势 $V(r)$ 为：
$[ V(r)=\dfrac {\rho }{8\pi {\varepsilon }_{0}r}({{R}_{2}}^{2}-{{R}_{1}}^{2})] $
根据高斯定律，对于一个均匀带电的球壳，其内部的电场强度可以通过考虑等效点电荷来计算。由于球壳内部的电场强度为零，因此空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电场强度为零。
步骤 2：计算空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电势
球壳的电势可以通过积分来求解，考虑球壳上的面电荷分布。由于球壳为均匀带电体，内外表面分别带有电荷，电势可以表示为：
$[ V(r)=\dfrac {\rho }{4\pi {\varepsilon }_{0}}{\int }_{{R}_{1}}^{{R}_{2}}\dfrac {r'}{r}dr'] $
其中，$r'$ 是球心到球壳上任意一点的距离。这个积分考虑了从内半径 $({R}_{1})$ 到外半径 $({R}_{2})$ 的电势贡献。具体计算步骤如下：
$[ V(r)=\dfrac {\rho }{4\pi {\varepsilon }_{0}r}[ \dfrac {{r}^{2}}{2}] }^{{R}_{1}}] $
$[ V(r)=\dfrac {\rho }{8\pi {\varepsilon }_{0}r}[ {{R}_{2}}^{2}-{{R}_{1}}^{2}] ] $
因此，空腔内距离球心为 $r(r\lt {R}_{1})$ 的任一点的电势 $V(r)$ 为：
$[ V(r)=\dfrac {\rho }{8\pi {\varepsilon }_{0}r}({{R}_{2}}^{2}-{{R}_{1}}^{2})] $