题目
1-7 在Oxy平面内有一个运动的质点,其运动函数为 =3ii+10(t)^2j(SI), 求:-|||-(1)t时刻的速度。-|||-(2)切向加速度和法向加速度的大小。-|||-(3)该质点运动的轨迹方程。

题目解答
答案
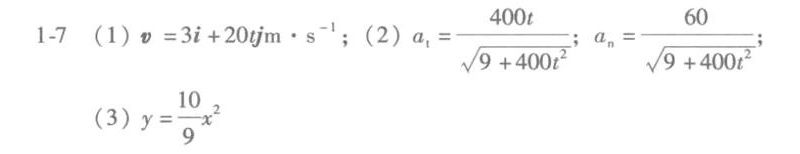
解析
步骤 1:求速度
速度是位置矢量对时间的导数。给定位置矢量 $r=3ti+10{t}^{2}j$,我们对时间t求导得到速度矢量 $v$。
$$
v = \frac{dr}{dt} = \frac{d}{dt}(3ti+10{t}^{2}j) = 3i + 20tj
$$
步骤 2:求加速度
加速度是速度矢量对时间的导数。给定速度矢量 $v=3i+20tj$,我们对时间t求导得到加速度矢量 $a$。
$$
a = \frac{dv}{dt} = \frac{d}{dt}(3i+20tj) = 20j
$$
步骤 3:求切向加速度和法向加速度
切向加速度是加速度在速度方向上的分量,法向加速度是加速度在速度垂直方向上的分量。速度矢量 $v=3i+20tj$,加速度矢量 $a=20j$。
切向加速度 ${a}_{t}$ 可以通过速度和加速度的点积除以速度的模来计算:
$$
{a}_{t} = \frac{v \cdot a}{|v|} = \frac{(3i+20tj) \cdot (20j)}{\sqrt{3^2 + (20t)^2}} = \frac{400t}{\sqrt{9+400{t}^{2}}}
$$
法向加速度 ${a}_{n}$ 可以通过加速度的模减去切向加速度的平方根来计算:
$$
{a}_{n} = \sqrt{|a|^2 - {a}_{t}^2} = \sqrt{20^2 - \left(\frac{400t}{\sqrt{9+400{t}^{2}}}\right)^2} = \frac{60}{\sqrt{9+400{t}^{2}}}
$$
步骤 4:求轨迹方程
轨迹方程可以通过消去时间t来得到。给定 $x=3t$ 和 $y=10{t}^{2}$,我们可以通过解第一个方程得到 $t=\frac{x}{3}$,然后将其代入第二个方程得到轨迹方程。
$$
y = 10\left(\frac{x}{3}\right)^2 = \frac{10}{9}{x}^{2}
$$
速度是位置矢量对时间的导数。给定位置矢量 $r=3ti+10{t}^{2}j$,我们对时间t求导得到速度矢量 $v$。
$$
v = \frac{dr}{dt} = \frac{d}{dt}(3ti+10{t}^{2}j) = 3i + 20tj
$$
步骤 2:求加速度
加速度是速度矢量对时间的导数。给定速度矢量 $v=3i+20tj$,我们对时间t求导得到加速度矢量 $a$。
$$
a = \frac{dv}{dt} = \frac{d}{dt}(3i+20tj) = 20j
$$
步骤 3:求切向加速度和法向加速度
切向加速度是加速度在速度方向上的分量,法向加速度是加速度在速度垂直方向上的分量。速度矢量 $v=3i+20tj$,加速度矢量 $a=20j$。
切向加速度 ${a}_{t}$ 可以通过速度和加速度的点积除以速度的模来计算:
$$
{a}_{t} = \frac{v \cdot a}{|v|} = \frac{(3i+20tj) \cdot (20j)}{\sqrt{3^2 + (20t)^2}} = \frac{400t}{\sqrt{9+400{t}^{2}}}
$$
法向加速度 ${a}_{n}$ 可以通过加速度的模减去切向加速度的平方根来计算:
$$
{a}_{n} = \sqrt{|a|^2 - {a}_{t}^2} = \sqrt{20^2 - \left(\frac{400t}{\sqrt{9+400{t}^{2}}}\right)^2} = \frac{60}{\sqrt{9+400{t}^{2}}}
$$
步骤 4:求轨迹方程
轨迹方程可以通过消去时间t来得到。给定 $x=3t$ 和 $y=10{t}^{2}$,我们可以通过解第一个方程得到 $t=\frac{x}{3}$,然后将其代入第二个方程得到轨迹方程。
$$
y = 10\left(\frac{x}{3}\right)^2 = \frac{10}{9}{x}^{2}
$$