题目
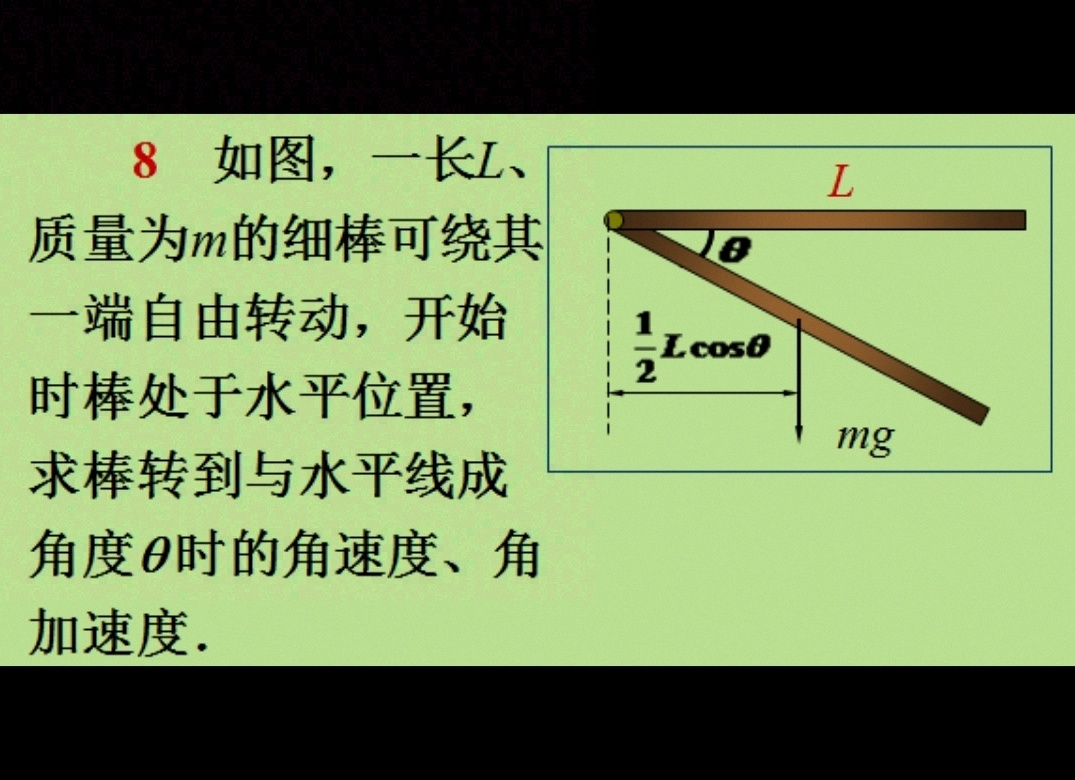
8 如图,一长L、 L-|||-质量为m的细棒可绕其-|||-一端自由转动,开始 1/2 L cosθ-|||-时棒处于水平位置,-|||-求棒转到与水平线成-|||-g-|||-角度θ时的角速度、角-|||-加速度.
题目解答
答案

解析
步骤 1:确定初始条件和能量守恒
细棒从水平位置开始自由转动,初始角速度为0。根据能量守恒定律,细棒的重力势能转化为转动动能。初始位置时,细棒的重力势能为$mg\frac{1}{2}L$,其中$g$是重力加速度,$L$是细棒的长度,$m$是细棒的质量。当细棒转到与水平线成$\theta$角度时,细棒的重力势能为$mg\frac{1}{2}L\cos\theta$。
步骤 2:计算角速度
根据能量守恒定律,细棒的重力势能变化等于转动动能的变化。即$mg\frac{1}{2}L(1-\cos\theta)=\frac{1}{2}I\omega^2$,其中$I$是细棒绕其一端的转动惯量,$\omega$是角速度。细棒绕其一端的转动惯量为$I=\frac{1}{3}mL^2$。将$I$代入上式,得到$mg\frac{1}{2}L(1-\cos\theta)=\frac{1}{2}\frac{1}{3}mL^2\omega^2$。化简得到$\omega=\sqrt{\frac{3g(1-\cos\theta)}{L}}$。
步骤 3:计算角加速度
根据牛顿第二定律,细棒的角加速度$a$与细棒所受的合外力矩$M$成正比,即$a=\frac{M}{I}$。细棒所受的合外力矩为$M=mg\frac{1}{2}L\sin\theta$。将$I$代入上式,得到$a=\frac{mg\frac{1}{2}L\sin\theta}{\frac{1}{3}mL^2}=\frac{3g\sin\theta}{2L}$。
细棒从水平位置开始自由转动,初始角速度为0。根据能量守恒定律,细棒的重力势能转化为转动动能。初始位置时,细棒的重力势能为$mg\frac{1}{2}L$,其中$g$是重力加速度,$L$是细棒的长度,$m$是细棒的质量。当细棒转到与水平线成$\theta$角度时,细棒的重力势能为$mg\frac{1}{2}L\cos\theta$。
步骤 2:计算角速度
根据能量守恒定律,细棒的重力势能变化等于转动动能的变化。即$mg\frac{1}{2}L(1-\cos\theta)=\frac{1}{2}I\omega^2$,其中$I$是细棒绕其一端的转动惯量,$\omega$是角速度。细棒绕其一端的转动惯量为$I=\frac{1}{3}mL^2$。将$I$代入上式,得到$mg\frac{1}{2}L(1-\cos\theta)=\frac{1}{2}\frac{1}{3}mL^2\omega^2$。化简得到$\omega=\sqrt{\frac{3g(1-\cos\theta)}{L}}$。
步骤 3:计算角加速度
根据牛顿第二定律,细棒的角加速度$a$与细棒所受的合外力矩$M$成正比,即$a=\frac{M}{I}$。细棒所受的合外力矩为$M=mg\frac{1}{2}L\sin\theta$。将$I$代入上式,得到$a=\frac{mg\frac{1}{2}L\sin\theta}{\frac{1}{3}mL^2}=\frac{3g\sin\theta}{2L}$。