题目
频率/组距-|||-0.032-|||-0.020-|||-0.018-|||-a-|||-0.010-|||-0.006-|||-0 40 50 60 70 80 90 100 成绩(分数)某学校在假期安排了“垃圾分类知识普及实践活动”．为了解学生的学习成果，该校对全校学生进行了测试(满分100分)，从中随机抽取50名学生的成绩，并将其分成以下6组：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，整理得到如图所示的频率分布直方图．(Ⅰ)求图中a的值；(Ⅱ)试估计全校学生的平均成绩；(同一组中的数据用该组区间的中点值作代表)(Ⅲ)将频率视为概率，从全校成绩在80分及以上的学生中随机抽取10人，用X表示成绩在[90，100]中的人数，求X的数学期望．
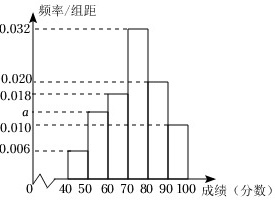某学校在假期安排了“垃圾分类知识普及实践活动”．为了解学生的学习成果，该校对全校学生进行了测试(满分100分)，从中随机抽取50名学生的成绩，并将其分成以下6组：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，整理得到如图所示的频率分布直方图．(Ⅰ)求图中a的值；
(Ⅱ)试估计全校学生的平均成绩；(同一组中的数据用该组区间的中点值作代表)
(Ⅲ)将频率视为概率，从全校成绩在80分及以上的学生中随机抽取10人，用X表示成绩在[90，100]中的人数，求X的数学期望．
题目解答
答案
解：(I)由题意得(0.006+a+0.018+0.032+0.02+0.01)×10=1，
解得a=0.014；
(II)由数据计算得$\overline{X}$=45×0.06+55×0.14+65×0.18+75×0.32+85×0.2+95×0.1=72.6，
(III)由题意在80分及以上的学生中抽取一人成绩在[90，100]中的概率为 $\frac{0.01}{0.02+0.01}=\frac{1}{3}$，抽取10人时，X～B(10，$\frac{1}{3}$)，
由二项分布知E(X)=10×$\frac{1}{3}=\frac{10}{3}$，D(X)=10×$\frac{1}{3}×\frac{2}{3}=\frac{20}{9}$．
解得a=0.014；
(II)由数据计算得$\overline{X}$=45×0.06+55×0.14+65×0.18+75×0.32+85×0.2+95×0.1=72.6，
(III)由题意在80分及以上的学生中抽取一人成绩在[90，100]中的概率为 $\frac{0.01}{0.02+0.01}=\frac{1}{3}$，抽取10人时，X～B(10，$\frac{1}{3}$)，
由二项分布知E(X)=10×$\frac{1}{3}=\frac{10}{3}$，D(X)=10×$\frac{1}{3}×\frac{2}{3}=\frac{20}{9}$．
解析
步骤 1：求解a的值
根据频率分布直方图的性质，所有组的频率之和等于1。因此，我们可以根据直方图中给出的频率值来求解a的值。
步骤 2：估计全校学生的平均成绩
根据频率分布直方图，我们可以计算出每个组的频率，然后用每个组的中点值乘以该组的频率，最后将所有组的乘积相加，得到全校学生的平均成绩。
步骤 3：求解X的数学期望
根据频率分布直方图，我们可以计算出成绩在80分及以上的学生中，成绩在[90，100]中的概率。然后，根据二项分布的性质，我们可以求解X的数学期望。
根据频率分布直方图的性质，所有组的频率之和等于1。因此，我们可以根据直方图中给出的频率值来求解a的值。
步骤 2：估计全校学生的平均成绩
根据频率分布直方图，我们可以计算出每个组的频率，然后用每个组的中点值乘以该组的频率，最后将所有组的乘积相加，得到全校学生的平均成绩。
步骤 3：求解X的数学期望
根据频率分布直方图，我们可以计算出成绩在80分及以上的学生中，成绩在[90，100]中的概率。然后，根据二项分布的性质，我们可以求解X的数学期望。