题目
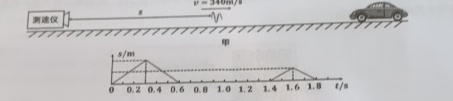
问题思考:你知道汽车是如何判断它与周围物体间的距离吗 ?情境二:生活中常用超声波测速仪来检测车速 ,其测速原理是测速仪前后两次发出并接收到被测车反射回的超声波信号, 再根据两次信号的时间差测出车速。某次测速中, 测速仪发出与接收超声波的情况如图乙所示, s 表示超声波与测速仪之间的距离, 假设超声波的速度为 340 m / s 且保持不变 . ( 1 ) 两 个超声波信号分别何时与汽车相遇?( 2 ) 在汽车与两个超声波相遇的时间点 汽车与测速仪之间的距离分别是多少 ?( 3 ) 汽车的速度是多少?v=340m/-|||-建仪-|||-7777777-|||-甲-|||-0.2 0.4 0.6 0.8 1. 0 1.2 6 1.8 t/s
问题思考:你知道汽车是如何判断它与周围物体间的距离吗 ?
情境二:生活中常用超声波测速仪来检测车速 ,其测速原理是测速仪前后两次发出并接收到被测车反射回的超声波信号, 再根据两次信号的时间差测出车速。某次测速中, 测速仪发出与接收超声波的情况如图乙所示, s 表示超声波与测速仪之间的距离, 假设超声波的速度为 340 m / s 且保持不变 .
( 1 ) 两 个超声波信号分别何时与汽车相遇?
( 2 ) 在汽车与两个超声波相遇的时间点 汽车与测速仪之间的距离分别是多少 ?
( 3 ) 汽车的速度是多少?
题目解答
答案
解:
(1)根据图乙即可得出:超声波在0.3s和1.6s时与汽车相遇;
(2)根据图乙:
在t=0.3s相遇时,两者之间的距离=(0.3-0)×340=102m
在t=1.6s相遇时,两者之间的距离=(1.6-1.4)×340=68m
(3)根据(2),得出v=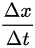 =
=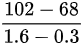 =26.15m/s
=26.15m/s
∥
解析
考查要点:本题主要考查超声波测速的原理,涉及匀速直线运动的计算,需要理解超声波传播时间与距离的关系,并能通过时间差计算物体运动速度。
解题核心思路:
- 确定超声波相遇时间:根据图乙中超声波信号的接收时间,直接读出两次相遇时刻。
- 计算相遇时距离:利用超声波速度公式 $s = v \cdot t$,结合相遇时间差计算距离。
- 求汽车速度:通过两次相遇时的距离差和时间差,应用速度公式 $v = \frac{\Delta s}{\Delta t}$ 计算。
破题关键点:
- 明确超声波传播时间:超声波从测速仪到汽车的单程时间对应相遇时刻。
- 正确处理时间差:两次相遇的时间间隔为总时间差,而非单程时间差。
(1)两个超声波信号分别何时与汽车相遇?
根据图乙中超声波信号的接收时间:
- 第一次相遇:超声波在 $t = 0.3\,\text{s}$ 时被汽车反射并被测速仪接收。
- 第二次相遇:超声波在 $t = 1.6\,\text{s}$ 时被汽车反射并被测速仪接收。
(2)汽车与测速仪的距离计算
第一次相遇($t = 0.3\,\text{s}$)
- 超声波传播时间:$0.3\,\text{s} - 0\,\text{s} = 0.3\,\text{s}$(假设第一次超声波在 $t = 0$ 发出)。
- 距离:$s_1 = v \cdot t = 340\,\text{m/s} \cdot 0.3\,\text{s} = 102\,\text{m}$。
第二次相遇($t = 1.6\,\text{s}$)
- 超声波传播时间:$1.6\,\text{s} - 1.4\,\text{s} = 0.2\,\text{s}$(假设第二次超声波在 $t = 1.4\,\text{s}$ 发出)。
- 距离:$s_2 = v \cdot t = 340\,\text{m/s} \cdot 0.2\,\text{s} = 68\,\text{m}$。
(3)汽车的速度计算
- 距离变化:$\Delta s = s_1 - s_2 = 102\,\text{m} - 68\,\text{m} = 34\,\text{m}$。
- 时间间隔:$\Delta t = 1.6\,\text{s} - 0.3\,\text{s} = 1.3\,\text{s}$。
- 速度:$v = \frac{\Delta s}{\Delta t} = \frac{34\,\text{m}}{1.3\,\text{s}} \approx 26.15\,\text{m/s}$。