题目
用波长500nm的单色光，垂直照射到一平面光栅上，测量第二级明纹的衍射角正弦500nm，求： ( 1 ) 光屏上出现条纹的最大级数，( 2 ) 当刻痕部分的宽度是透光部分的两倍时，光屏上共能出现明条纹的条数。
用波长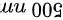
的单色光，垂直照射到一平面光栅上，测量第二级明纹的衍射角正弦
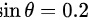，求： ( 1 ) 光屏上出现条纹的最大级数，( 2 ) 当刻痕部分的宽度是透光部分的两倍时，光屏上共能出现明条纹的条数。
题目解答
答案
（1）
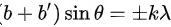，可得
，
，
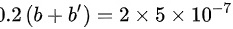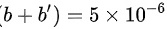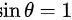时，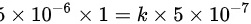
，
。
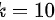（2）
。
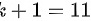解析
步骤 1：确定光栅方程
光栅方程为$(b+b')\sin \theta = k\lambda$，其中$b$是透光部分的宽度，$b'$是刻痕部分的宽度，$\theta$是衍射角，$k$是级数，$\lambda$是光的波长。
步骤 2：计算光栅常数
根据题目条件，第二级明纹的衍射角正弦$\sin \theta =0.2$，波长$\lambda =500nm=5\times {10}^{-7}m$，代入光栅方程$(b+b')\sin \theta = k\lambda$，得到$(b+b')\times 0.2 = 2\times 5\times {10}^{-7}$，从而计算出$(b+b')=5\times {10}^{-6}m$。
步骤 3：计算最大级数
当$\sin \theta =1$时，光屏上出现条纹的级数最大，代入光栅方程$(b+b')\sin \theta = k\lambda$，得到$5\times {10}^{-6}\times 1=k\times 5\times {10}^{-7}$，从而计算出$k=10$。
步骤 4：计算明条纹的条数
当刻痕部分的宽度是透光部分的两倍时，即$b'=2b$，代入$(b+b')=5\times {10}^{-6}$，得到$3b=5\times {10}^{-6}$，从而计算出$b=\frac{5}{3}\times {10}^{-6}$，$b'=2b=\frac{10}{3}\times {10}^{-6}$。根据光栅方程$(b+b')\sin \theta = k\lambda$，当$\sin \theta =1$时，$k$最大，代入计算出$k=10$。由于明条纹出现在$k$的正负值，所以光屏上共能出现明条纹的条数为$2k+1=21$。
光栅方程为$(b+b')\sin \theta = k\lambda$，其中$b$是透光部分的宽度，$b'$是刻痕部分的宽度，$\theta$是衍射角，$k$是级数，$\lambda$是光的波长。
步骤 2：计算光栅常数
根据题目条件，第二级明纹的衍射角正弦$\sin \theta =0.2$，波长$\lambda =500nm=5\times {10}^{-7}m$，代入光栅方程$(b+b')\sin \theta = k\lambda$，得到$(b+b')\times 0.2 = 2\times 5\times {10}^{-7}$，从而计算出$(b+b')=5\times {10}^{-6}m$。
步骤 3：计算最大级数
当$\sin \theta =1$时，光屏上出现条纹的级数最大，代入光栅方程$(b+b')\sin \theta = k\lambda$，得到$5\times {10}^{-6}\times 1=k\times 5\times {10}^{-7}$，从而计算出$k=10$。
步骤 4：计算明条纹的条数
当刻痕部分的宽度是透光部分的两倍时，即$b'=2b$，代入$(b+b')=5\times {10}^{-6}$，得到$3b=5\times {10}^{-6}$，从而计算出$b=\frac{5}{3}\times {10}^{-6}$，$b'=2b=\frac{10}{3}\times {10}^{-6}$。根据光栅方程$(b+b')\sin \theta = k\lambda$，当$\sin \theta =1$时，$k$最大，代入计算出$k=10$。由于明条纹出现在$k$的正负值，所以光屏上共能出现明条纹的条数为$2k+1=21$。