题目
2-3-2 若恒定电场中有非均匀的导电媒质(其电导率-|||-y=y(x,y,z) ,介电常数 varepsilon =e(x,y,z)) ,求媒质中自由-|||-电荷的体密度。

题目解答
答案
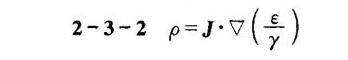
解析
步骤 1:理解问题
题目要求我们求解在非均匀导电媒质中自由电荷的体密度。已知电导率 $\sigma = \sigma(x,y,z)$ 和介电常数 $\varepsilon = \varepsilon(x,y,z)$。
步骤 2:应用麦克斯韦方程组
在恒定电场中,电位移矢量 $\mathbf{D}$ 和电场强度 $\mathbf{E}$ 之间的关系为 $\mathbf{D} = \varepsilon \mathbf{E}$。同时,电流密度 $\mathbf{J}$ 与电场强度 $\mathbf{E}$ 之间的关系为 $\mathbf{J} = \sigma \mathbf{E}$。根据麦克斯韦方程组中的高斯定律,自由电荷的体密度 $\rho$ 与电位移矢量 $\mathbf{D}$ 之间的关系为 $\nabla \cdot \mathbf{D} = \rho$。
步骤 3:计算自由电荷的体密度
将 $\mathbf{D} = \varepsilon \mathbf{E}$ 代入 $\nabla \cdot \mathbf{D} = \rho$,得到 $\nabla \cdot (\varepsilon \mathbf{E}) = \rho$。由于 $\mathbf{J} = \sigma \mathbf{E}$,可以将 $\mathbf{E}$ 表示为 $\mathbf{E} = \frac{\mathbf{J}}{\sigma}$。将 $\mathbf{E}$ 的表达式代入 $\nabla \cdot (\varepsilon \mathbf{E}) = \rho$,得到 $\nabla \cdot (\varepsilon \frac{\mathbf{J}}{\sigma}) = \rho$。进一步化简得到 $\rho = \nabla \cdot (\frac{\varepsilon}{\sigma} \mathbf{J})$。
题目要求我们求解在非均匀导电媒质中自由电荷的体密度。已知电导率 $\sigma = \sigma(x,y,z)$ 和介电常数 $\varepsilon = \varepsilon(x,y,z)$。
步骤 2:应用麦克斯韦方程组
在恒定电场中,电位移矢量 $\mathbf{D}$ 和电场强度 $\mathbf{E}$ 之间的关系为 $\mathbf{D} = \varepsilon \mathbf{E}$。同时,电流密度 $\mathbf{J}$ 与电场强度 $\mathbf{E}$ 之间的关系为 $\mathbf{J} = \sigma \mathbf{E}$。根据麦克斯韦方程组中的高斯定律,自由电荷的体密度 $\rho$ 与电位移矢量 $\mathbf{D}$ 之间的关系为 $\nabla \cdot \mathbf{D} = \rho$。
步骤 3:计算自由电荷的体密度
将 $\mathbf{D} = \varepsilon \mathbf{E}$ 代入 $\nabla \cdot \mathbf{D} = \rho$,得到 $\nabla \cdot (\varepsilon \mathbf{E}) = \rho$。由于 $\mathbf{J} = \sigma \mathbf{E}$,可以将 $\mathbf{E}$ 表示为 $\mathbf{E} = \frac{\mathbf{J}}{\sigma}$。将 $\mathbf{E}$ 的表达式代入 $\nabla \cdot (\varepsilon \mathbf{E}) = \rho$,得到 $\nabla \cdot (\varepsilon \frac{\mathbf{J}}{\sigma}) = \rho$。进一步化简得到 $\rho = \nabla \cdot (\frac{\varepsilon}{\sigma} \mathbf{J})$。