题目
9.设x1,x2,x3是来自总体X的样本,若 (X)=u (未知), hat (mu )=dfrac (1)(2)(x)_(1)-a(x)_(2)+3a(x)_(3) 是μ的-|||-无偏估计,则常数 a=-|||-A. dfrac (1)(6) B. dfrac (1)(4) C. dfrac (1)(3) D. dfrac (1)(2)
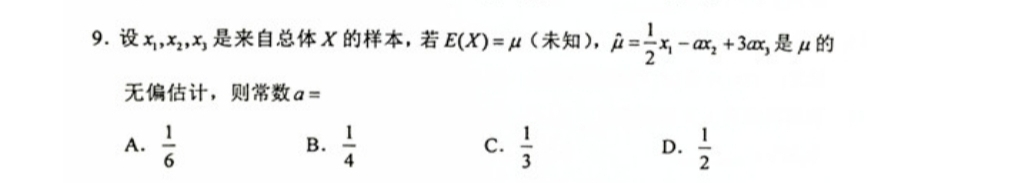
题目解答
答案

解析
步骤 1:确定无偏估计的条件
无偏估计的条件是估计量的期望值等于总体参数的期望值。即 $E(\hat{a}) = E(\mu)$。
步骤 2:计算估计量的期望值
根据题目给出的估计量 $\hat{a} = \dfrac{1}{2}x_1 - ax_2 + 3ax_3$,我们计算其期望值:
$E(\hat{a}) = E(\dfrac{1}{2}x_1 - ax_2 + 3ax_3)$
$= \dfrac{1}{2}E(x_1) - aE(x_2) + 3aE(x_3)$
由于 $x_1, x_2, x_3$ 是来自总体 $X$ 的样本,且 $E(X) = \mu$,所以 $E(x_1) = E(x_2) = E(x_3) = \mu$。
$E(\hat{a}) = \dfrac{1}{2}\mu - a\mu + 3a\mu$
$= (\dfrac{1}{2} + 2a)\mu$
步骤 3:根据无偏估计的条件求解常数 a
根据无偏估计的条件,$E(\hat{a}) = \mu$,所以有:
$(\dfrac{1}{2} + 2a)\mu = \mu$
解得:$\dfrac{1}{2} + 2a = 1$
$2a = \dfrac{1}{2}$
$a = \dfrac{1}{4}$
无偏估计的条件是估计量的期望值等于总体参数的期望值。即 $E(\hat{a}) = E(\mu)$。
步骤 2:计算估计量的期望值
根据题目给出的估计量 $\hat{a} = \dfrac{1}{2}x_1 - ax_2 + 3ax_3$,我们计算其期望值:
$E(\hat{a}) = E(\dfrac{1}{2}x_1 - ax_2 + 3ax_3)$
$= \dfrac{1}{2}E(x_1) - aE(x_2) + 3aE(x_3)$
由于 $x_1, x_2, x_3$ 是来自总体 $X$ 的样本,且 $E(X) = \mu$,所以 $E(x_1) = E(x_2) = E(x_3) = \mu$。
$E(\hat{a}) = \dfrac{1}{2}\mu - a\mu + 3a\mu$
$= (\dfrac{1}{2} + 2a)\mu$
步骤 3:根据无偏估计的条件求解常数 a
根据无偏估计的条件,$E(\hat{a}) = \mu$,所以有:
$(\dfrac{1}{2} + 2a)\mu = \mu$
解得:$\dfrac{1}{2} + 2a = 1$
$2a = \dfrac{1}{2}$
$a = \dfrac{1}{4}$