题目
(本题10分)质量为M1=24 kg的圆轮,可绕水平光滑固定轴转动,一轻绳缠绕于轮上,另一端通过质量为M2=5 kg的圆盘形定滑轮悬有m=10 kg的物体.求当重物由静止开始下降了h=0.5 m时,(1) 物体的速度;(2) 绳中张力.(设绳与定滑轮间无相对滑动,圆轮、定滑轮绕通过轮心且垂直于横截面的水平光滑轴的转动惯量分别为,)
(本题10分)
质量为M1=24 kg的圆轮,可绕水平光滑固定轴转动,一轻绳缠绕于轮上,另一端通过质量为M2=5 kg的圆盘形定滑轮悬有m=10 kg的物体.求当重物由静止开始下降了h=0.5 m时,
(1) 物体的速度;
(2) 绳中张力.
(设绳与定滑轮间无相对滑动,圆轮、定滑轮绕通过轮心且垂直于横截面的水平光滑轴的转动惯量分别为,)
题目解答
答案
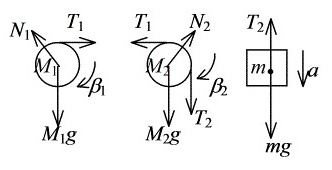
解:各物体的受力情况如图所示.
由转动定律、牛顿第二定律及运动学方程,可列出以下联立方程:
T1R=J11=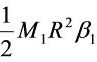
T2r-T1r=J22=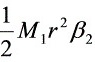
mg-T2=ma , a=R1=r2 , v 2=2ah
 求解联立方程,得
求解联立方程,得 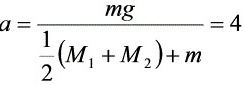 m/s2
m/s2
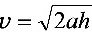 =2 m/s
=2 m/s
T2=m(g-a)=58 N
T1=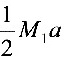 =48 N
=48 N
解析
步骤 1:确定各物体的受力情况
物体m受到重力mg和绳子的拉力T2,圆轮M1受到绳子的拉力T1,定滑轮M2受到绳子的拉力T1和T2。由于绳子是轻质的,所以绳子的拉力在不同位置是相同的。
步骤 2:列出各物体的运动方程
对于物体m,根据牛顿第二定律,有:mg - T2 = ma
对于圆轮M1,根据转动定律,有:T1R = J1α1,其中J1是圆轮的转动惯量,α1是圆轮的角加速度。
对于定滑轮M2,根据转动定律,有:T2r - T1r = J2α2,其中J2是定滑轮的转动惯量,α2是定滑轮的角加速度。
由于绳子与定滑轮间无相对滑动,所以物体m的加速度a等于圆轮M1的线加速度,即a = Rα1 = rα2。
步骤 3:联立方程求解
联立以上方程,可以求解出物体m的加速度a,进而求出物体m的速度v和绳子的拉力T1和T2。
物体m受到重力mg和绳子的拉力T2,圆轮M1受到绳子的拉力T1,定滑轮M2受到绳子的拉力T1和T2。由于绳子是轻质的,所以绳子的拉力在不同位置是相同的。
步骤 2:列出各物体的运动方程
对于物体m,根据牛顿第二定律,有:mg - T2 = ma
对于圆轮M1,根据转动定律,有:T1R = J1α1,其中J1是圆轮的转动惯量,α1是圆轮的角加速度。
对于定滑轮M2,根据转动定律,有:T2r - T1r = J2α2,其中J2是定滑轮的转动惯量,α2是定滑轮的角加速度。
由于绳子与定滑轮间无相对滑动,所以物体m的加速度a等于圆轮M1的线加速度,即a = Rα1 = rα2。
步骤 3:联立方程求解
联立以上方程,可以求解出物体m的加速度a,进而求出物体m的速度v和绳子的拉力T1和T2。