题目
"一颗子弹由枪口射出时速率为(v)_(0)mcdot (s)^-1,当子弹在枪筒内被加速时,它所受的合方为F=(a-bt)N(a,b为常数),其中t以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量;(3)求子弹的质量."
"
一颗子弹由枪口射出时速率为${v}_{0}m\cdot {s}^{-1}$,当子弹在枪筒内被加速时,它所受的合方为$F=(a-bt)N$(a,b为常数),其中t以秒为单位:
(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;
(2)求子弹所受的冲量;
(3)求子弹的质量.
"题目解答
答案
"
【答案】
(1)$\dfrac{a}{b}$;(2)$\dfrac{{a}^{2}}{2b}$;(3)$\dfrac{{a}^{2}}{2b{v}_{0}}$
【解析】
(1)设子弹走完枪筒全长所需时间为t,由合力公式,令$F=0$可得$a-bt=0$,即$t=\dfrac{a}{b}$;
(2)根据冲量的定义,画出力和时间之间的关系图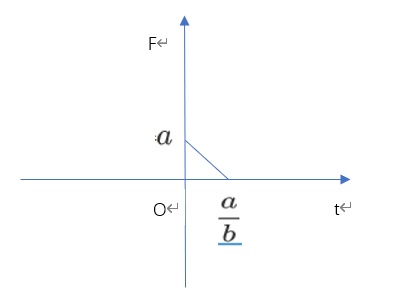 ;
;
根据冲量定义$\stackrel{}{I}=\stackrel{}{F}\cdot t$,计算图中三角形的面积就是冲量的大小$I=\dfrac{1}{2}\times a\times \dfrac{a}{b}=\dfrac{{a}^{2}}{2b}$,与速度方向一致;
(3)由动量定理,设子弹的质量为m,则有$I=m{v}_{0}$,可得$m=\dfrac{{a}^{2}}{2b{v}_{0}}$。
"解析
(1)设子弹走完枪筒全长所需时间为t,由合力公式,令$F=0$可得$a-bt=0$,即$t=\dfrac{a}{b}$;
(2)根据冲量的定义,画出力和时间之间的关系图F← a O← $\dfrac {a}{b}$ té;
根据冲量定义$\stackrel{}{I}=\stackrel{}{F}\cdot t$,计算图中三角形的面积就是冲量的大小$I=\dfrac{1}{2}\times a\times \dfrac{a}{b}=\dfrac{{a}^{2}}{2b}$,与速度方向一致;
(3)由动量定理,设子弹的质量为m,则有$I=m{v}_{0}$,可得$m=\dfrac{{a}^{2}}{2b{v}_{0}}$。
"
【解析】
步骤 1:计算子弹走完枪筒全长所需时间
根据题目中给出的合力公式$F=(a-bt)$,当子弹运行到枪口处合力刚好为零,即$F=0$,可以得到$a-bt=0$,解得$t=\dfrac{a}{b}$。
步骤 2:计算子弹所受的冲量
根据冲量的定义,冲量$I=\int_{0}^{t}Fdt$,将$F=(a-bt)$代入,得到$I=\int_{0}^{\frac{a}{b}}(a-bt)dt$,计算得$I=\dfrac{1}{2}\times a\times \dfrac{a}{b}=\dfrac{{a}^{2}}{2b}$。
步骤 3:计算子弹的质量
根据动量定理,$I=m{v}_{0}$,将$I=\dfrac{{a}^{2}}{2b}$代入,得到$m=\dfrac{{a}^{2}}{2b{v}_{0}}$。
(2)根据冲量的定义,画出力和时间之间的关系图F← a O← $\dfrac {a}{b}$ té;
根据冲量定义$\stackrel{}{I}=\stackrel{}{F}\cdot t$,计算图中三角形的面积就是冲量的大小$I=\dfrac{1}{2}\times a\times \dfrac{a}{b}=\dfrac{{a}^{2}}{2b}$,与速度方向一致;
(3)由动量定理,设子弹的质量为m,则有$I=m{v}_{0}$,可得$m=\dfrac{{a}^{2}}{2b{v}_{0}}$。
"
【解析】
步骤 1:计算子弹走完枪筒全长所需时间
根据题目中给出的合力公式$F=(a-bt)$,当子弹运行到枪口处合力刚好为零,即$F=0$,可以得到$a-bt=0$,解得$t=\dfrac{a}{b}$。
步骤 2:计算子弹所受的冲量
根据冲量的定义,冲量$I=\int_{0}^{t}Fdt$,将$F=(a-bt)$代入,得到$I=\int_{0}^{\frac{a}{b}}(a-bt)dt$,计算得$I=\dfrac{1}{2}\times a\times \dfrac{a}{b}=\dfrac{{a}^{2}}{2b}$。
步骤 3:计算子弹的质量
根据动量定理,$I=m{v}_{0}$,将$I=\dfrac{{a}^{2}}{2b}$代入,得到$m=\dfrac{{a}^{2}}{2b{v}_{0}}$。