题目
一物体做直线运动,运动方程为=6(t)^2-2(t)^3,式中各量均采用国际单位制,求:(1)第二秒内的平均速度;(2)第三秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
一物体做直线运动,运动方程为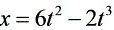
,式中各量均采用国际单位制,求:
(1)第二秒内的平均速度;
(2)第三秒末的速度;
(3)第一秒末的加速度;
(4)物体运动的类型。
题目解答
答案
解: 由于: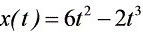 
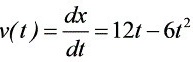
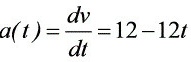
所以:(1)第二秒内的平均速度:
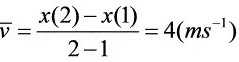
(2)第三秒末的速度:
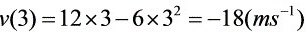
(3)第一秒末的加速度:
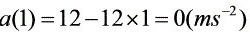
(4)物体运动的类型为变速直线运动。
解析
步骤 1：计算第二秒内的平均速度
根据运动方程$x=6{t}^{2}-2{t}^{3}$，计算$t=1$秒和$t=2$秒时的位置$x(1)$和$x(2)$，然后利用平均速度公式$\overline {v}=\dfrac {x(2)-x(1)}{2-1}$计算第二秒内的平均速度。
步骤 2：计算第三秒末的速度
根据运动方程$x=6{t}^{2}-2{t}^{3}$，求导得到速度方程$v(t)=\dfrac {dx}{dt}=12t-6{t}^{2}$，然后代入$t=3$秒计算第三秒末的速度$v(3)$。
步骤 3：计算第一秒末的加速度
根据速度方程$v(t)=12t-6{t}^{2}$，求导得到加速度方程$a(t)=\dfrac {dv}{dt}=12-12t$，然后代入$t=1$秒计算第一秒末的加速度$a(1)$。
步骤 4：确定物体运动的类型
根据加速度方程$a(t)=12-12t$，判断加速度是否为常数，从而确定物体运动的类型。
根据运动方程$x=6{t}^{2}-2{t}^{3}$，计算$t=1$秒和$t=2$秒时的位置$x(1)$和$x(2)$，然后利用平均速度公式$\overline {v}=\dfrac {x(2)-x(1)}{2-1}$计算第二秒内的平均速度。
步骤 2：计算第三秒末的速度
根据运动方程$x=6{t}^{2}-2{t}^{3}$，求导得到速度方程$v(t)=\dfrac {dx}{dt}=12t-6{t}^{2}$，然后代入$t=3$秒计算第三秒末的速度$v(3)$。
步骤 3：计算第一秒末的加速度
根据速度方程$v(t)=12t-6{t}^{2}$，求导得到加速度方程$a(t)=\dfrac {dv}{dt}=12-12t$，然后代入$t=1$秒计算第一秒末的加速度$a(1)$。
步骤 4：确定物体运动的类型
根据加速度方程$a(t)=12-12t$，判断加速度是否为常数，从而确定物体运动的类型。