题目
如图甲所示,某科技小组的同学用弹簧测力计悬挂一实心圆柱形金属块,使其缓慢匀速下降,并将其浸入平静的游泳池水中,弹簧测力计的示数F与金属块下底面下降高度h的变化关系如图乙所示,忽略金属块浸入水中时池水液面高度的变化,g取10N/kg,则下列说法中正确的是( )square THATIMM.-|||-甲-|||-↑F/N-|||-46-|||-26-|||-0 30 50 70 h/cm A. 金属块所受重力大小为26N B. 金属块的密度为2.3×103kg/m3 C. 金属块完全浸没在水中时所受浮力的大小为26N D. 金属块恰好完全浸没时,金属块下底面所受水的压强为5×103Pa
如图甲所示,某科技小组的同学用弹簧测力计悬挂一实心圆柱形金属块,使其缓慢匀速下降,并将其浸入平静的游泳池水中,弹簧测力计的示数F与金属块下底面下降高度h的变化关系如图乙所示,忽略金属块浸入水中时池水液面高度的变化,g取10N/kg,则下列说法中正确的是( )
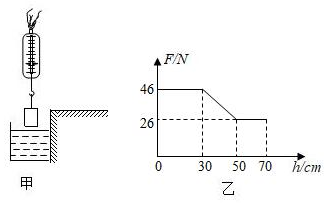

- A. 金属块所受重力大小为26N
- B. 金属块的密度为2.3×103kg/m3
- C. 金属块完全浸没在水中时所受浮力的大小为26N
- D. 金属块恰好完全浸没时,金属块下底面所受水的压强为5×103Pa
题目解答
答案
解:
A、由图象可知,当h=0时,弹簧测力计示数为46N,此时金属块处于空气中,根据二力平衡条件可知,金属块的重力:G=F拉1=46N;故A错;
BC、金属块的质量:
m=$\frac{G}{g}$=$\frac{46N}{10N/kg}$=4.6kg;
由图象可知,当h=50cm之后,弹簧测力计示数不变,金属块浸没水中,受到的浮力:F浮=G-F拉2=46N-26N=20N;
由F浮=ρ液gV排可得金属块体积:
V=V排=$\frac{{F}_{浮}}{{ρ}_{水}g}$=$\frac{20N}{1×1{0}^{3}kg/{m}^{3}×10N/kg}$=2×10-3m3,
金属块的密度:
ρ=$\frac{m}{V}$=$\frac{4.6kg}{2×1{0}^{-3}{m}^{3}}$=2.3×103kg/m3,故B正确、C错;
D、金属块刚浸没时下表面距水面距离:h=50cm-30cm=20cm=0.2m,
金属块下底面受到水的压强:
p=ρ水gh=1×103kg/m3×10N/kg×0.2m=2×103Pa,故D错。
故选:B。
A、由图象可知,当h=0时,弹簧测力计示数为46N,此时金属块处于空气中,根据二力平衡条件可知,金属块的重力:G=F拉1=46N;故A错;
BC、金属块的质量:
m=$\frac{G}{g}$=$\frac{46N}{10N/kg}$=4.6kg;
由图象可知,当h=50cm之后,弹簧测力计示数不变,金属块浸没水中,受到的浮力:F浮=G-F拉2=46N-26N=20N;
由F浮=ρ液gV排可得金属块体积:
V=V排=$\frac{{F}_{浮}}{{ρ}_{水}g}$=$\frac{20N}{1×1{0}^{3}kg/{m}^{3}×10N/kg}$=2×10-3m3,
金属块的密度:
ρ=$\frac{m}{V}$=$\frac{4.6kg}{2×1{0}^{-3}{m}^{3}}$=2.3×103kg/m3,故B正确、C错;
D、金属块刚浸没时下表面距水面距离:h=50cm-30cm=20cm=0.2m,
金属块下底面受到水的压强:
p=ρ水gh=1×103kg/m3×10N/kg×0.2m=2×103Pa,故D错。
故选:B。
解析
步骤 1:确定金属块的重力
由图象可知,当h=0时,弹簧测力计示数为46N,此时金属块处于空气中,根据二力平衡条件可知,金属块的重力:G=F_拉1=46N;故A错;
步骤 2:计算金属块的密度
由图象可知,当h=50cm之后,弹簧测力计示数不变,金属块浸没水中,受到的浮力:F_浮=G-F_拉2=46N-26N=20N;
由F_浮=ρ_液gV_排可得金属块体积:
V=V_排=$\frac{{F}_{浮}}{{ρ}_{水}g}$=$\frac{20N}{1×1{0}^{3}kg/{m}^{3}×10N/kg}$=2×10^{-3}m^{3},
金属块的质量:
m=$\frac{G}{g}$=$\frac{46N}{10N/kg}$=4.6kg,
金属块的密度:
ρ=$\frac{m}{V}$=$\frac{4.6kg}{2×1{0}^{-3}{m}^{3}}$=2.3×10^{3}kg/m^{3},故B正确、C错;
步骤 3:计算金属块下底面所受水的压强
金属块刚浸没时下表面距水面距离:h=50cm-30cm=20cm=0.2m,
金属块下底面受到水的压强:
p=ρ_水gh=1×10^{3}kg/m^{3}×10N/kg×0.2m=2×10^{3}Pa,故D错。
由图象可知,当h=0时,弹簧测力计示数为46N,此时金属块处于空气中,根据二力平衡条件可知,金属块的重力:G=F_拉1=46N;故A错;
步骤 2:计算金属块的密度
由图象可知,当h=50cm之后,弹簧测力计示数不变,金属块浸没水中,受到的浮力:F_浮=G-F_拉2=46N-26N=20N;
由F_浮=ρ_液gV_排可得金属块体积:
V=V_排=$\frac{{F}_{浮}}{{ρ}_{水}g}$=$\frac{20N}{1×1{0}^{3}kg/{m}^{3}×10N/kg}$=2×10^{-3}m^{3},
金属块的质量:
m=$\frac{G}{g}$=$\frac{46N}{10N/kg}$=4.6kg,
金属块的密度:
ρ=$\frac{m}{V}$=$\frac{4.6kg}{2×1{0}^{-3}{m}^{3}}$=2.3×10^{3}kg/m^{3},故B正确、C错;
步骤 3:计算金属块下底面所受水的压强
金属块刚浸没时下表面距水面距离:h=50cm-30cm=20cm=0.2m,
金属块下底面受到水的压强:
p=ρ_水gh=1×10^{3}kg/m^{3}×10N/kg×0.2m=2×10^{3}Pa,故D错。