题目
1.频率为1000Hz的波,波速为 /s, 试求:-|||-(1)相为差为 dfrac (pi )(3) 的两点之间的距离;-|||-(2)在某点处时间间隔为 ^-3s 的两个振动状态间的相位差。

题目解答
答案
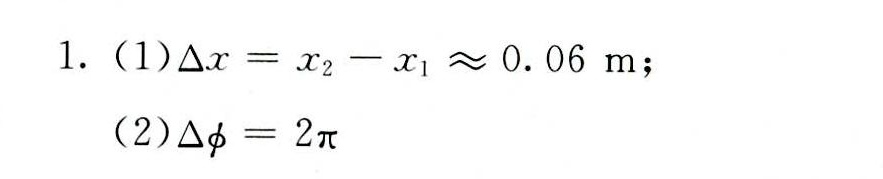
解析
步骤 1:计算波长
根据波速公式 $v = f \lambda$,其中 $v$ 是波速,$f$ 是频率,$\lambda$ 是波长。将已知的波速和频率代入公式,可以计算出波长。
步骤 2:计算相位差为 $\dfrac {\pi }{3}$ 的两点之间的距离
相位差 $\Delta \phi$ 与两点之间的距离 $\Delta x$ 之间的关系为 $\Delta \phi = \dfrac {2\pi}{\lambda} \Delta x$。将已知的相位差和波长代入公式,可以计算出两点之间的距离。
步骤 3:计算时间间隔为 ${10}^{-3}s$ 的两个振动状态间的相位差
相位差 $\Delta \phi$ 与时间间隔 $\Delta t$ 之间的关系为 $\Delta \phi = 2\pi f \Delta t$。将已知的频率和时间间隔代入公式,可以计算出相位差。
根据波速公式 $v = f \lambda$,其中 $v$ 是波速,$f$ 是频率,$\lambda$ 是波长。将已知的波速和频率代入公式,可以计算出波长。
步骤 2:计算相位差为 $\dfrac {\pi }{3}$ 的两点之间的距离
相位差 $\Delta \phi$ 与两点之间的距离 $\Delta x$ 之间的关系为 $\Delta \phi = \dfrac {2\pi}{\lambda} \Delta x$。将已知的相位差和波长代入公式,可以计算出两点之间的距离。
步骤 3:计算时间间隔为 ${10}^{-3}s$ 的两个振动状态间的相位差
相位差 $\Delta \phi$ 与时间间隔 $\Delta t$ 之间的关系为 $\Delta \phi = 2\pi f \Delta t$。将已知的频率和时间间隔代入公式,可以计算出相位差。