题目
某医院收治糖尿病患者108名,随机分两组每组各54人,用甲乙两种不同治疗方法,血糖控制率甲组为74.1%,乙组为51.9%人,^2=5.72,则结论应该为（）A.甲方法和乙方法血糖控制率相同B.甲方法和乙方法血糖控制率无差异C.甲方法和乙方法血糖控制率有差异D.无法判断统计学结果E.甲方法和乙方法血糖控制率差异无统计学意义
某医院收治糖尿病患者108名,随机分两组每组各54人,用甲乙两种不同治疗方法,血糖控制率甲组为74.1%,乙组为51.9%人,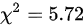
,则结论应该为（）
A.甲方法和乙方法血糖控制率相同
B.甲方法和乙方法血糖控制率无差异
C.甲方法和乙方法血糖控制率有差异
D.无法判断统计学结果
E.甲方法和乙方法血糖控制率差异无统计学意义
题目解答
答案
本题答案为：C
由题可知，糖尿病患者总数：108名
分组情况：甲组54人，乙组54人。血糖控制率：甲组74.1%，乙组51.9%，。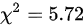
首先明确假设检验的基本原理：
在这个问题中，我们是在比较两种治疗方法（甲和乙）对血糖控制率是否有差异。
我们设定的原假设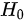
是两种方法血糖控制率相同，备择假设
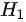是两种方法血糖控制率不同。
然后看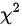
检验的结果,已知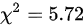，对于自由度
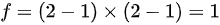（这里是四格表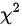检验，R=2行，C=2列），查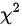临界值表，当
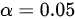时，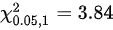
。
由于5.72>3.84，因此P<0.05。
最后得出结论，拒绝原假设，接受备择假设，即甲方法和乙方法血糖控制率有差异。
所以，本题答案是C
解析
步骤 1：设定假设
- 原假设H0：甲方法和乙方法血糖控制率相同。
- 备择假设H1：甲方法和乙方法血糖控制率不同。
步骤 2：计算${x}^{2}$值
- 已知${x}^{2}=5.72$。
步骤 3：确定自由度和临界值
- 自由度$f=(2-1)\times (2-1)=1$（四格表${x}^{2}$检验，R=2行，C=2列）。
- 查${x}^{2}$临界值表，当$90'0=x$时，${{x}_{0}}^{2}0.05,1=3.84$。
步骤 4：比较${x}^{2}$值和临界值
- 由于5.72>3.84，因此P<0.05。
步骤 5：得出结论
- 拒绝原假设，接受备择假设，即甲方法和乙方法血糖控制率有差异。
- 原假设H0：甲方法和乙方法血糖控制率相同。
- 备择假设H1：甲方法和乙方法血糖控制率不同。
步骤 2：计算${x}^{2}$值
- 已知${x}^{2}=5.72$。
步骤 3：确定自由度和临界值
- 自由度$f=(2-1)\times (2-1)=1$（四格表${x}^{2}$检验，R=2行，C=2列）。
- 查${x}^{2}$临界值表，当$90'0=x$时，${{x}_{0}}^{2}0.05,1=3.84$。
步骤 4：比较${x}^{2}$值和临界值
- 由于5.72>3.84，因此P<0.05。
步骤 5：得出结论
- 拒绝原假设，接受备择假设，即甲方法和乙方法血糖控制率有差异。