题目
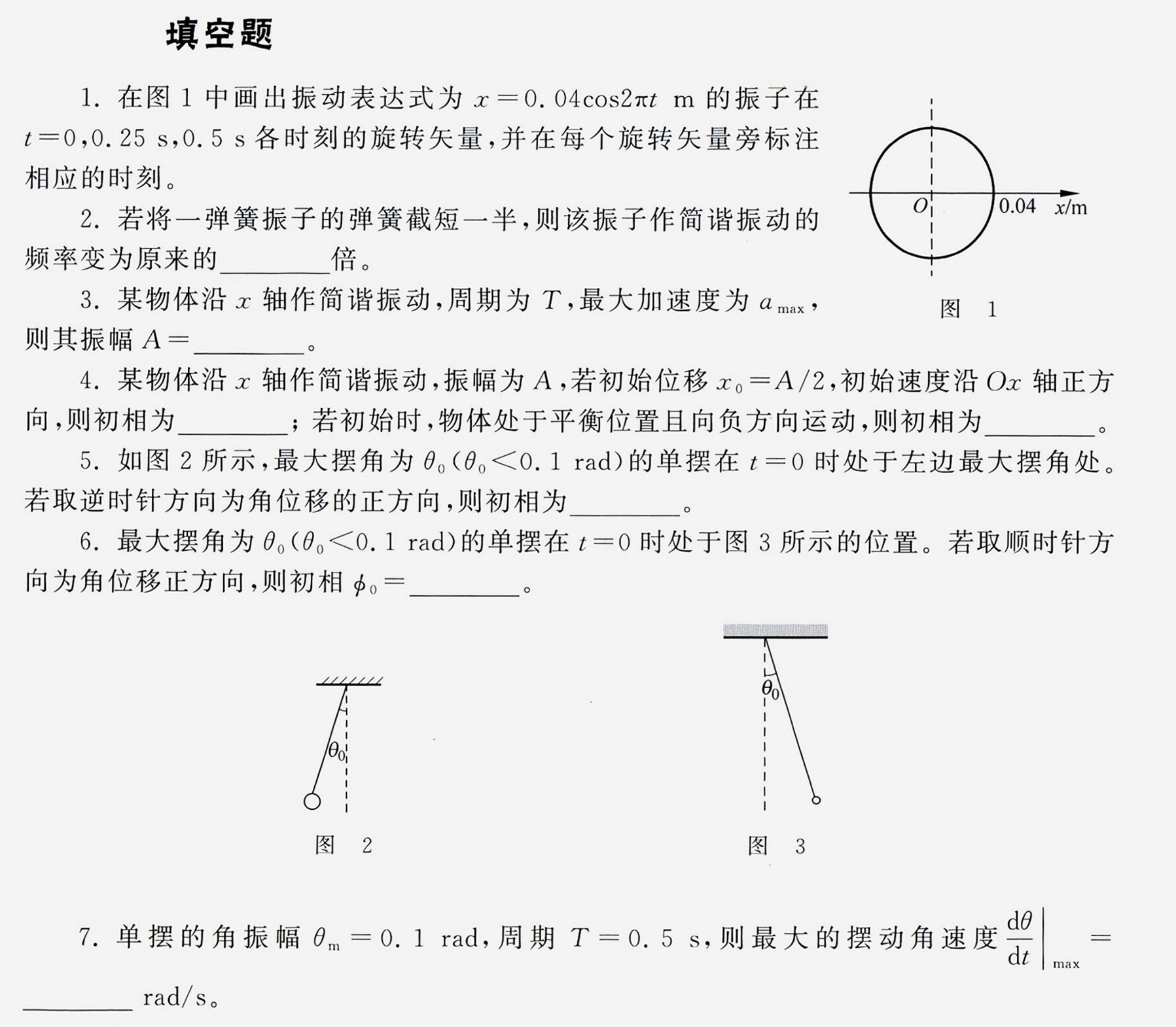
填空题-|||-1.在图1中画出振动表达式为 =0.04cos 2pi tm 的振子在-|||-.t=0 ,0.25s,0.5s各时刻的旋转矢量,并在每个旋转矢量旁标注-|||-相应的时刻。-|||-0.04 x/m-|||-1-|||-图 1-|||-2.若将一弹簧振子的弹簧截短一半,则该振子作简谐振动的-|||-频率变为原来的 __ 倍。-|||-3.某物体沿x轴作简谐振动,周期为T,最大加速度为amax,-|||-则其振幅 A= __-|||-4.某物体沿x轴作简谐振动,振幅为A,若初始位移 _(0)=A/2 ,初始速度沿Ox轴正方-|||-向,则初相为 __ ;若初始时,物体处于平衡位置且向负方向运动,则初相为 __-|||-5.如图2所示,最大摆角为θ0( (theta )_(0)lt 0.1rad )的单摆在 t=0 时处于左边最大摆角处。-|||-若取逆时针方向为角位移的正方向,则初相为 __ o-|||-6.最大摆角为θ。( (theta )_(0)lt 0.1rad )的单摆在 t=0 时处于图3所示的位置。若取顺时针方-|||-向为角位移正方向,则初相 (varphi )_(0)= __ o-|||-θ-|||-图 2 图 3-|||-7.单摆的角振幅 (theta )_(m)=0.1rad ,周期 T=0.5s ,则最大的摆动角速度 dfrac (dtheta )(dt)(int )_(max)=-|||-__ _rad/s 。
题目解答
答案

解析
步骤 1:旋转矢量的绘制
旋转矢量的长度等于振幅,旋转矢量的角速度等于振动的角频率。对于振动表达式 $x=0.04\cos 2\pi tm$,振幅为0.04m,角频率为$2\pi$ rad/s。在t=0, 0.25s, 0.5s时,旋转矢量分别指向x轴正方向、y轴正方向、x轴负方向。
步骤 2:频率变化
弹簧振子的频率$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$,其中k是弹簧的劲度系数,m是振子的质量。当弹簧截短一半时,劲度系数k变为原来的2倍,因此频率变为原来的$\sqrt{2}$倍。
步骤 3:振幅计算
最大加速度$a_{max}=A\omega^2$,其中A是振幅,$\omega$是角频率。因此,振幅$A=\frac{a_{max}}{\omega^2}=\frac{a_{max}T^2}{4\pi^2}$。
步骤 4:初相计算
当初始位移$x_0=A/2$,初始速度沿Ox轴正方向时,初相为$-\frac{\pi}{3}$。当初始时,物体处于平衡位置且向负方向运动时,初相为$\pi/2$。
步骤 5:单摆初相计算
当单摆在t=0时处于左边最大摆角处,且取逆时针方向为角位移的正方向时,初相为$\pi$。当单摆在t=0时处于图3所示的位置,且取顺时针方向为角位移正方向时,初相为$\pi$。
步骤 6:最大摆动角速度计算
最大摆动角速度$\frac{d\theta}{dt}_{max}=\theta_m\omega=\theta_m\frac{2\pi}{T}$,其中$\theta_m$是角振幅,T是周期。因此,最大摆动角速度为$0.1rad\times\frac{2\pi}{0.5s}=0.4\pi rad/s$。
旋转矢量的长度等于振幅,旋转矢量的角速度等于振动的角频率。对于振动表达式 $x=0.04\cos 2\pi tm$,振幅为0.04m,角频率为$2\pi$ rad/s。在t=0, 0.25s, 0.5s时,旋转矢量分别指向x轴正方向、y轴正方向、x轴负方向。
步骤 2:频率变化
弹簧振子的频率$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$,其中k是弹簧的劲度系数,m是振子的质量。当弹簧截短一半时,劲度系数k变为原来的2倍,因此频率变为原来的$\sqrt{2}$倍。
步骤 3:振幅计算
最大加速度$a_{max}=A\omega^2$,其中A是振幅,$\omega$是角频率。因此,振幅$A=\frac{a_{max}}{\omega^2}=\frac{a_{max}T^2}{4\pi^2}$。
步骤 4:初相计算
当初始位移$x_0=A/2$,初始速度沿Ox轴正方向时,初相为$-\frac{\pi}{3}$。当初始时,物体处于平衡位置且向负方向运动时,初相为$\pi/2$。
步骤 5:单摆初相计算
当单摆在t=0时处于左边最大摆角处,且取逆时针方向为角位移的正方向时,初相为$\pi$。当单摆在t=0时处于图3所示的位置,且取顺时针方向为角位移正方向时,初相为$\pi$。
步骤 6:最大摆动角速度计算
最大摆动角速度$\frac{d\theta}{dt}_{max}=\theta_m\omega=\theta_m\frac{2\pi}{T}$,其中$\theta_m$是角振幅,T是周期。因此,最大摆动角速度为$0.1rad\times\frac{2\pi}{0.5s}=0.4\pi rad/s$。