题目
化简n sqrt ({(1+{x)^2)}^3}=。
化简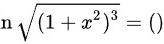 。
。
题目解答
答案
由题意得,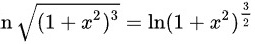
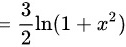 。
。
解析
步骤 1:识别根号内的表达式
题目中给出的表达式为 $\sqrt {{(1+{x}^{2})}^{3}}$,这是一个根号内的三次方表达式。
步骤 2:应用对数的性质
根据对数的性质,$\sqrt {{(1+{x}^{2})}^{3}}$ 可以写成 $\ln {(1+{x}^{2})}^{\dfrac {3}{2}}$。这是因为 $\sqrt{a} = a^{\frac{1}{2}}$,所以 $\sqrt {{(1+{x}^{2})}^{3}} = {(1+{x}^{2})}^{\frac{3}{2}}$,再应用对数的幂的性质 $\ln a^b = b \ln a$。
步骤 3:化简表达式
根据对数的幂的性质,$\ln {(1+{x}^{2})}^{\dfrac {3}{2}}$ 可以进一步化简为 $\dfrac {3}{2}\ln (1+{x}^{2})$。
题目中给出的表达式为 $\sqrt {{(1+{x}^{2})}^{3}}$,这是一个根号内的三次方表达式。
步骤 2:应用对数的性质
根据对数的性质,$\sqrt {{(1+{x}^{2})}^{3}}$ 可以写成 $\ln {(1+{x}^{2})}^{\dfrac {3}{2}}$。这是因为 $\sqrt{a} = a^{\frac{1}{2}}$,所以 $\sqrt {{(1+{x}^{2})}^{3}} = {(1+{x}^{2})}^{\frac{3}{2}}$,再应用对数的幂的性质 $\ln a^b = b \ln a$。
步骤 3:化简表达式
根据对数的幂的性质,$\ln {(1+{x}^{2})}^{\dfrac {3}{2}}$ 可以进一步化简为 $\dfrac {3}{2}\ln (1+{x}^{2})$。