题目
如图所示,滑轮转动惯量为0.01kg . m{}^2 半径为7cm ;物体的质量为5kg,用一细绳与劲度系数k = 200N/m的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计。求: (1) 当绳拉直、弹簧无伸长时使物体由静止而下落的最大距离;(2) 物体的速m度达最大值时的位置及最大速率。
如图所示,滑轮转动惯量为$$0.01kg . m{}^{2} $$半径为7cm ;物体的质量为5kg,用一细绳与劲度系数$$k = 200N/m$$的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计。求:
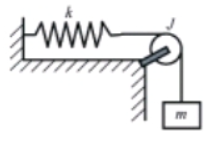
(1) 当绳拉直、弹簧无伸长时使物体由静止而下落的最大距离;
(2) 物体的速m度达最大值时的位置及最大速率。
题目解答
答案
(1) 0.5m
(2) 0.25m;1.58m/s
解析
步骤 1:确定物体下落的最大距离
物体下落时,重力势能转化为弹簧的弹性势能和滑轮的转动动能。当物体下落最大距离时,物体速度为零,动能为零,此时重力势能完全转化为弹簧的弹性势能。
步骤 2:计算物体下落最大距离
设物体下落的最大距离为$$x$$,则物体的重力势能变化为$$mgx$$,弹簧的弹性势能变化为$$\frac{1}{2}kx^2$$,滑轮的转动动能为$$\frac{1}{2}I\omega^2$$,其中$$I$$为滑轮的转动惯量,$$\omega$$为滑轮的角速度。由于绳与滑轮间无相对滑动,物体的速度$$v$$与滑轮的角速度$$\omega$$满足$$v = r\omega$$,其中$$r$$为滑轮的半径。因此,滑轮的转动动能可以表示为$$\frac{1}{2}I\frac{v^2}{r^2}$$。当物体下落最大距离时,物体速度为零,动能为零,此时重力势能完全转化为弹簧的弹性势能,即$$mgx = \frac{1}{2}kx^2$$。解此方程可得物体下落的最大距离$$x$$。
步骤 3:确定物体速度达最大值时的位置及最大速率
物体速度达最大值时,物体的重力势能和弹簧的弹性势能之和最小,此时物体的重力势能变化为$$mgx$$,弹簧的弹性势能变化为$$\frac{1}{2}kx^2$$,滑轮的转动动能为$$\frac{1}{2}I\omega^2$$。由于绳与滑轮间无相对滑动,物体的速度$$v$$与滑轮的角速度$$\omega$$满足$$v = r\omega$$,其中$$r$$为滑轮的半径。因此,滑轮的转动动能可以表示为$$\frac{1}{2}I\frac{v^2}{r^2}$$。物体速度达最大值时,物体的重力势能和弹簧的弹性势能之和最小,即$$mgx = \frac{1}{2}kx^2 + \frac{1}{2}I\frac{v^2}{r^2}$$。解此方程可得物体速度达最大值时的位置$$x$$及最大速率$$v$$。
物体下落时,重力势能转化为弹簧的弹性势能和滑轮的转动动能。当物体下落最大距离时,物体速度为零,动能为零,此时重力势能完全转化为弹簧的弹性势能。
步骤 2:计算物体下落最大距离
设物体下落的最大距离为$$x$$,则物体的重力势能变化为$$mgx$$,弹簧的弹性势能变化为$$\frac{1}{2}kx^2$$,滑轮的转动动能为$$\frac{1}{2}I\omega^2$$,其中$$I$$为滑轮的转动惯量,$$\omega$$为滑轮的角速度。由于绳与滑轮间无相对滑动,物体的速度$$v$$与滑轮的角速度$$\omega$$满足$$v = r\omega$$,其中$$r$$为滑轮的半径。因此,滑轮的转动动能可以表示为$$\frac{1}{2}I\frac{v^2}{r^2}$$。当物体下落最大距离时,物体速度为零,动能为零,此时重力势能完全转化为弹簧的弹性势能,即$$mgx = \frac{1}{2}kx^2$$。解此方程可得物体下落的最大距离$$x$$。
步骤 3:确定物体速度达最大值时的位置及最大速率
物体速度达最大值时,物体的重力势能和弹簧的弹性势能之和最小,此时物体的重力势能变化为$$mgx$$,弹簧的弹性势能变化为$$\frac{1}{2}kx^2$$,滑轮的转动动能为$$\frac{1}{2}I\omega^2$$。由于绳与滑轮间无相对滑动,物体的速度$$v$$与滑轮的角速度$$\omega$$满足$$v = r\omega$$,其中$$r$$为滑轮的半径。因此,滑轮的转动动能可以表示为$$\frac{1}{2}I\frac{v^2}{r^2}$$。物体速度达最大值时,物体的重力势能和弹簧的弹性势能之和最小,即$$mgx = \frac{1}{2}kx^2 + \frac{1}{2}I\frac{v^2}{r^2}$$。解此方程可得物体速度达最大值时的位置$$x$$及最大速率$$v$$。