题目
已知=f(dfrac (3x-2)(3x+2));=f(dfrac (3x-2)(3x+2));则=f(dfrac (3x-2)(3x+2))等于多少?
已知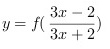
;
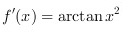;则
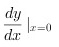等于多少?
题目解答
答案
令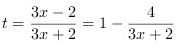
则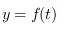
求得: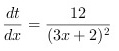
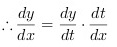
$$={\rm arctan }({3x-2\over 3x+2})^2\cdot {12\over (3x+2)^2}$$
所以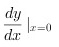$$={\rm arctan}1\cdot 3=3{\rm arctan }1$$
解析
步骤 1：定义变量
令$t=\dfrac {3x-2}{3x+2}=1-\dfrac {4}{3x+2}$，则$y=f(t)$。
步骤 2：求导
求得$\dfrac {dt}{dx}=\dfrac {12}{{(3x+2)}^{2}}$。
步骤 3：应用链式法则
根据链式法则，$\dfrac {dy}{dx}=\dfrac {dy}{dt}\cdot \dfrac {dt}{dx}$。
步骤 4：代入$f'(x)$
代入$f'(x)=\arctan {x}^{2}$，得到$\dfrac {dy}{dx}={\rm arctan }({3x-2\over 3x+2})^2\cdot {12\over (3x+2)^2}$。
步骤 5：计算$x=0$时的导数
将$x=0$代入$\dfrac {dy}{dx}$，得到$\dfrac {dy}{dx}{|}_{x}=0={\rm arctan}1\cdot 3=3{\rm arctan }1$。
令$t=\dfrac {3x-2}{3x+2}=1-\dfrac {4}{3x+2}$，则$y=f(t)$。
步骤 2：求导
求得$\dfrac {dt}{dx}=\dfrac {12}{{(3x+2)}^{2}}$。
步骤 3：应用链式法则
根据链式法则，$\dfrac {dy}{dx}=\dfrac {dy}{dt}\cdot \dfrac {dt}{dx}$。
步骤 4：代入$f'(x)$
代入$f'(x)=\arctan {x}^{2}$，得到$\dfrac {dy}{dx}={\rm arctan }({3x-2\over 3x+2})^2\cdot {12\over (3x+2)^2}$。
步骤 5：计算$x=0$时的导数
将$x=0$代入$\dfrac {dy}{dx}$，得到$\dfrac {dy}{dx}{|}_{x}=0={\rm arctan}1\cdot 3=3{\rm arctan }1$。