题目
在图示直角坐标系中,F=200kN,力F与x轴的夹角为45°,则该力在x轴上的投影大小为( )y↑-|||-F-|||-45-|||-0-|||-xA.y↑-|||-F-|||-45-|||-0-|||-xB.y↑-|||-F-|||-45-|||-0-|||-xC.200kND.100kN
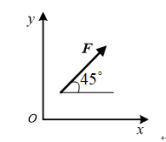
在图示直角坐标系中,F=200kN,力F与x轴的夹角为45°,则该力在x轴上的投影大小为( )
- A.
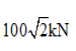
- B.
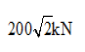
- C.200kN
- D.100kN
题目解答
答案
A
解析
步骤 1:确定力F在x轴上的投影
力F在x轴上的投影大小可以通过力F的大小和它与x轴的夹角来计算。力F在x轴上的投影大小等于力F的大小乘以cos(45°)。
步骤 2:计算力F在x轴上的投影大小
力F的大小为200kN,与x轴的夹角为45°。因此,力F在x轴上的投影大小为$200kN \times \cos(45°)$。
步骤 3:计算cos(45°)的值
$\cos(45°) = \frac{\sqrt{2}}{2}$。
步骤 4:计算力F在x轴上的投影大小
$200kN \times \cos(45°) = 200kN \times \frac{\sqrt{2}}{2} = 100\sqrt{2}kN$。
力F在x轴上的投影大小可以通过力F的大小和它与x轴的夹角来计算。力F在x轴上的投影大小等于力F的大小乘以cos(45°)。
步骤 2:计算力F在x轴上的投影大小
力F的大小为200kN,与x轴的夹角为45°。因此,力F在x轴上的投影大小为$200kN \times \cos(45°)$。
步骤 3:计算cos(45°)的值
$\cos(45°) = \frac{\sqrt{2}}{2}$。
步骤 4:计算力F在x轴上的投影大小
$200kN \times \cos(45°) = 200kN \times \frac{\sqrt{2}}{2} = 100\sqrt{2}kN$。