题目
【题文】一辆汽车沿直线从甲地开往乙地,前一半位移内的平均速度为30km /h ,后一半位移内的平均速度是60km /h ,这辆汽车全程的平均速度是多少?.
【题文】一辆汽车沿直线从甲地开往乙地,前一半位移内的平均速度为30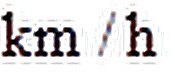
km /h
,后一半位移内的平均速度是60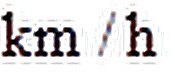
km /h
,这辆汽车全程的平均速度是多少?.题目解答
答案
【答案】40km/h
.解析
步骤 1:定义变量
设甲地到乙地的总位移为 \(2s\),则前一半位移为 \(s\),后一半位移也为 \(s\)。前一半位移的平均速度为 \(v_1 = 30 \text{ km/h}\),后一半位移的平均速度为 \(v_2 = 60 \text{ km/h}\)。
步骤 2:计算时间
前一半位移的时间为 \(t_1 = \frac{s}{v_1} = \frac{s}{30}\)。
后一半位移的时间为 \(t_2 = \frac{s}{v_2} = \frac{s}{60}\)。
步骤 3:计算总时间
总时间为 \(t = t_1 + t_2 = \frac{s}{30} + \frac{s}{60} = \frac{2s + s}{60} = \frac{3s}{60} = \frac{s}{20}\)。
步骤 4:计算全程平均速度
全程平均速度 \(v_{\text{avg}} = \frac{\text{总位移}}{\text{总时间}} = \frac{2s}{\frac{s}{20}} = 2s \times \frac{20}{s} = 40 \text{ km/h}\)。
设甲地到乙地的总位移为 \(2s\),则前一半位移为 \(s\),后一半位移也为 \(s\)。前一半位移的平均速度为 \(v_1 = 30 \text{ km/h}\),后一半位移的平均速度为 \(v_2 = 60 \text{ km/h}\)。
步骤 2:计算时间
前一半位移的时间为 \(t_1 = \frac{s}{v_1} = \frac{s}{30}\)。
后一半位移的时间为 \(t_2 = \frac{s}{v_2} = \frac{s}{60}\)。
步骤 3:计算总时间
总时间为 \(t = t_1 + t_2 = \frac{s}{30} + \frac{s}{60} = \frac{2s + s}{60} = \frac{3s}{60} = \frac{s}{20}\)。
步骤 4:计算全程平均速度
全程平均速度 \(v_{\text{avg}} = \frac{\text{总位移}}{\text{总时间}} = \frac{2s}{\frac{s}{20}} = 2s \times \frac{20}{s} = 40 \text{ km/h}\)。