题目
(2)已知 (int )_(0)^1f(x)dx=(int )_(0)^1xf(x)dx f(x)dxdy(其中 :x+yleqslant 1,xgeqslant 0,ygeqslant 0) 等于-|||-()-|||-(A)2. (B)0. (C) dfrac (1)(2). (D)1.
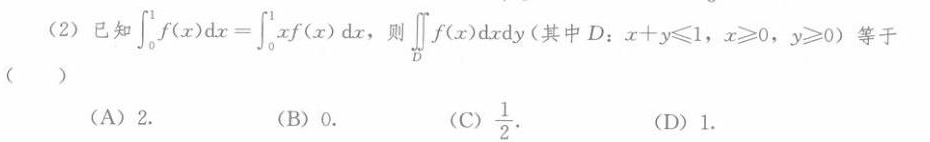
题目解答
答案
解析
步骤 1:理解已知条件
已知条件是 ${\int }_{0}^{1}f(x)dx={\int }_{0}^{1}xf(x)dx$,这意味着函数 $f(x)$ 在区间 $[0,1]$ 上的积分与 $xf(x)$ 在同一区间上的积分相等。
步骤 2:分析二重积分
二重积分 $\iint f(x)dxdy$ 在区域 $D$ 上,其中 $D$ 是由 $x+y\leqslant 1$,$x\geqslant 0$,$y\geqslant 0$ 定义的三角形区域。这个区域可以表示为 $0\leqslant x\leqslant 1$ 和 $0\leqslant y\leqslant 1-x$。
步骤 3:计算二重积分
根据二重积分的定义,我们可以将二重积分表示为:
$$\iint f(x)dxdy = \int_{0}^{1} \int_{0}^{1-x} f(x) dy dx$$
由于 $f(x)$ 与 $y$ 无关,我们可以将 $f(x)$ 提出积分号外:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) \left( \int_{0}^{1-x} dy \right) dx$$
内层积分 $\int_{0}^{1-x} dy$ 等于 $1-x$,因此:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) (1-x) dx$$
根据已知条件 ${\int }_{0}^{1}f(x)dx={\int }_{0}^{1}xf(x)dx$,我们可以将上式重写为:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) dx - \int_{0}^{1} xf(x) dx = 0$$
已知条件是 ${\int }_{0}^{1}f(x)dx={\int }_{0}^{1}xf(x)dx$,这意味着函数 $f(x)$ 在区间 $[0,1]$ 上的积分与 $xf(x)$ 在同一区间上的积分相等。
步骤 2:分析二重积分
二重积分 $\iint f(x)dxdy$ 在区域 $D$ 上,其中 $D$ 是由 $x+y\leqslant 1$,$x\geqslant 0$,$y\geqslant 0$ 定义的三角形区域。这个区域可以表示为 $0\leqslant x\leqslant 1$ 和 $0\leqslant y\leqslant 1-x$。
步骤 3:计算二重积分
根据二重积分的定义,我们可以将二重积分表示为:
$$\iint f(x)dxdy = \int_{0}^{1} \int_{0}^{1-x} f(x) dy dx$$
由于 $f(x)$ 与 $y$ 无关,我们可以将 $f(x)$ 提出积分号外:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) \left( \int_{0}^{1-x} dy \right) dx$$
内层积分 $\int_{0}^{1-x} dy$ 等于 $1-x$,因此:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) (1-x) dx$$
根据已知条件 ${\int }_{0}^{1}f(x)dx={\int }_{0}^{1}xf(x)dx$,我们可以将上式重写为:
$$\iint f(x)dxdy = \int_{0}^{1} f(x) dx - \int_{0}^{1} xf(x) dx = 0$$