题目
可见光的波长范围是 400 nm - 760 nm 用平行的白光垂直入射在平面透射光栅此光栅上 1 cm 刻了 500 条 刻痕试分析能看到几级清晰的可见光光谱。 ( 1 nm = 10 ^ -9 m )
可见光的波长范围是 400 nm - 760 nm 用平行的白光垂直入射在平面透射光栅此光栅上 1 cm 刻了 500 条 刻痕试分析能看到几级清晰的可见光光谱。 ( 1 nm = 10 ^ -9 m )
题目解答
答案
据题意,有光栅常数
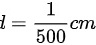
根据光栅方程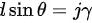
垂直入射θ=90°,j=1,2,3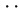 代入解得
代入解得
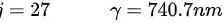
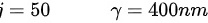
可见级数从27级开始到50级结束,因此可见级数
50-27+1=24
共24级
解析
步骤 1:计算光栅常数
光栅常数 $d$ 是指光栅上相邻两条刻痕之间的距离。根据题目,光栅上 1 cm 刻了 500 条刻痕,因此光栅常数 $d$ 为:
$$
d = \frac{1}{500} \text{ cm} = \frac{1}{500} \times 10^7 \text{ nm} = 20000 \text{ nm}
$$
步骤 2:应用光栅方程
光栅方程为 $d \sin \theta = m \lambda$,其中 $d$ 是光栅常数,$\theta$ 是衍射角,$m$ 是衍射级数,$\lambda$ 是光的波长。题目中提到光垂直入射,因此 $\theta = 90^\circ$,$\sin \theta = 1$。所以光栅方程简化为:
$$
d = m \lambda
$$
步骤 3:计算可见光谱的级数范围
根据题目,可见光的波长范围是 400 nm - 760 nm。将波长范围代入光栅方程,计算出对应的衍射级数 $m$。
对于 $\lambda = 760 \text{ nm}$:
$$
m = \frac{d}{\lambda} = \frac{20000 \text{ nm}}{760 \text{ nm}} \approx 26.32
$$
对于 $\lambda = 400 \text{ nm}$:
$$
m = \frac{d}{\lambda} = \frac{20000 \text{ nm}}{400 \text{ nm}} = 50
$$
因此,可见光谱的级数范围从 27 级到 50 级。
步骤 4:计算可见光谱的级数数量
可见光谱的级数数量为:
$$
50 - 27 + 1 = 24
$$
光栅常数 $d$ 是指光栅上相邻两条刻痕之间的距离。根据题目,光栅上 1 cm 刻了 500 条刻痕,因此光栅常数 $d$ 为:
$$
d = \frac{1}{500} \text{ cm} = \frac{1}{500} \times 10^7 \text{ nm} = 20000 \text{ nm}
$$
步骤 2:应用光栅方程
光栅方程为 $d \sin \theta = m \lambda$,其中 $d$ 是光栅常数,$\theta$ 是衍射角,$m$ 是衍射级数,$\lambda$ 是光的波长。题目中提到光垂直入射,因此 $\theta = 90^\circ$,$\sin \theta = 1$。所以光栅方程简化为:
$$
d = m \lambda
$$
步骤 3:计算可见光谱的级数范围
根据题目,可见光的波长范围是 400 nm - 760 nm。将波长范围代入光栅方程,计算出对应的衍射级数 $m$。
对于 $\lambda = 760 \text{ nm}$:
$$
m = \frac{d}{\lambda} = \frac{20000 \text{ nm}}{760 \text{ nm}} \approx 26.32
$$
对于 $\lambda = 400 \text{ nm}$:
$$
m = \frac{d}{\lambda} = \frac{20000 \text{ nm}}{400 \text{ nm}} = 50
$$
因此,可见光谱的级数范围从 27 级到 50 级。
步骤 4:计算可见光谱的级数数量
可见光谱的级数数量为:
$$
50 - 27 + 1 = 24
$$