题目
摆锤质量为m,半径为r,摆杆质量也为m,长度为2r,求整个钟摆的转动惯量。
摆锤质量为m,半径为r,摆杆质量也为m,长度为2r,求整个钟摆的转动惯量。
题目解答
答案
根据平行轴定理
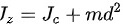
得圆盘的转动惯量.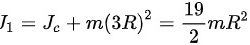 ,
,
根据转动惯量公式
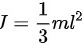
得细杆的转动惯量。
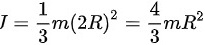
所以组合刚体的转动惯量为:
整个钟摆的转动惯量为
解析
步骤 1:计算摆锤的转动惯量
摆锤是一个圆盘,其质量为m,半径为r。圆盘绕中心轴的转动惯量公式为${I}_{c}=\dfrac{1}{2}m{r}^{2}$。由于摆锤的转动轴在圆盘的边缘,根据平行轴定理,摆锤的转动惯量为${I}_{1}={I}_{c}+m{d}^{2}=\dfrac{1}{2}m{r}^{2}+m{(3r)}^{2}=\dfrac{1}{2}m{r}^{2}+9m{r}^{2}=\dfrac{19}{2}m{r}^{2}$。
步骤 2:计算摆杆的转动惯量
摆杆是一个细杆,其质量为m,长度为2r。细杆绕一端的转动惯量公式为${I}_{2}=\dfrac{1}{3}m{l}^{2}$。将摆杆的长度代入公式,得到摆杆的转动惯量为${I}_{2}=\dfrac{1}{3}m{(2r)}^{2}=\dfrac{4}{3}m{r}^{2}$。
步骤 3:计算整个钟摆的转动惯量
整个钟摆的转动惯量为摆锤和摆杆的转动惯量之和,即${I}_{总}={I}_{1}+{I}_{2}=\dfrac{19}{2}m{r}^{2}+\dfrac{4}{3}m{r}^{2}=\dfrac{57}{6}m{r}^{2}+\dfrac{8}{6}m{r}^{2}=\dfrac{65}{6}m{r}^{2}$。
摆锤是一个圆盘,其质量为m,半径为r。圆盘绕中心轴的转动惯量公式为${I}_{c}=\dfrac{1}{2}m{r}^{2}$。由于摆锤的转动轴在圆盘的边缘,根据平行轴定理,摆锤的转动惯量为${I}_{1}={I}_{c}+m{d}^{2}=\dfrac{1}{2}m{r}^{2}+m{(3r)}^{2}=\dfrac{1}{2}m{r}^{2}+9m{r}^{2}=\dfrac{19}{2}m{r}^{2}$。
步骤 2:计算摆杆的转动惯量
摆杆是一个细杆,其质量为m,长度为2r。细杆绕一端的转动惯量公式为${I}_{2}=\dfrac{1}{3}m{l}^{2}$。将摆杆的长度代入公式,得到摆杆的转动惯量为${I}_{2}=\dfrac{1}{3}m{(2r)}^{2}=\dfrac{4}{3}m{r}^{2}$。
步骤 3:计算整个钟摆的转动惯量
整个钟摆的转动惯量为摆锤和摆杆的转动惯量之和,即${I}_{总}={I}_{1}+{I}_{2}=\dfrac{19}{2}m{r}^{2}+\dfrac{4}{3}m{r}^{2}=\dfrac{57}{6}m{r}^{2}+\dfrac{8}{6}m{r}^{2}=\dfrac{65}{6}m{r}^{2}$。