题目
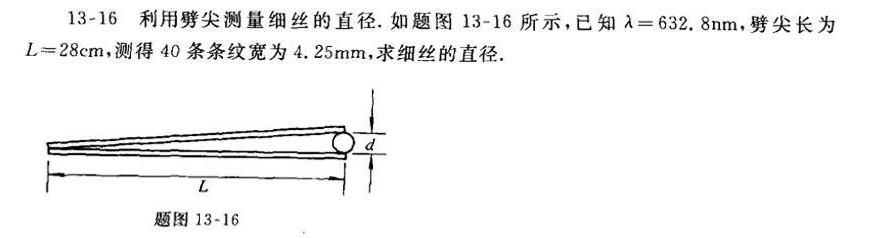
13-16 利用劈尖测量细丝的直径.如题图 13-16 所示,已知 lambda =632.8mm, 劈尖长为-|||-=28cm, 测得40条条纹宽为4.25mm,求细丝的直径.-|||-d-|||-L-|||-题图 13-16
题目解答
答案
解析
步骤 1:确定条纹宽度
已知40条条纹的总宽度为4.25mm,因此每条条纹的宽度为:
$$
\Delta x = \frac{4.25mm}{40} = 0.10625mm
$$
步骤 2:应用劈尖干涉公式
劈尖干涉的条纹宽度公式为:
$$
\Delta x = \frac{\lambda L}{d}
$$
其中,$\lambda$ 是光的波长,$L$ 是劈尖的长度,$d$ 是细丝的直径。将已知值代入公式中,得到:
$$
0.10625mm = \frac{632.8mm \times 28cm}{d}
$$
步骤 3:求解细丝的直径
将公式中的单位统一为毫米,即 $L=280mm$,然后解方程求得细丝的直径 $d$:
$$
d = \frac{632.8mm \times 280mm}{0.10625mm} = 1.68 \times 10^6mm^2
$$
$$
d = 8.13 \times 10^{-4}m
$$
已知40条条纹的总宽度为4.25mm,因此每条条纹的宽度为:
$$
\Delta x = \frac{4.25mm}{40} = 0.10625mm
$$
步骤 2:应用劈尖干涉公式
劈尖干涉的条纹宽度公式为:
$$
\Delta x = \frac{\lambda L}{d}
$$
其中,$\lambda$ 是光的波长,$L$ 是劈尖的长度,$d$ 是细丝的直径。将已知值代入公式中,得到:
$$
0.10625mm = \frac{632.8mm \times 28cm}{d}
$$
步骤 3:求解细丝的直径
将公式中的单位统一为毫米,即 $L=280mm$,然后解方程求得细丝的直径 $d$:
$$
d = \frac{632.8mm \times 280mm}{0.10625mm} = 1.68 \times 10^6mm^2
$$
$$
d = 8.13 \times 10^{-4}m
$$