题目
100名学生知识测试成绩的频数直方图-|||-频数 40-|||-0 ()-|||-o-|||-0 15 15-|||-10-|||-0 50 60 70 80 90 100 成绩(分)今年5月15日，亚洲文明对话大会在北京开幕．为了增进学生对亚洲文化的了解，某学校开展了相关知识的宣传教育活动．为了解这次宣传活动的效果，学校从全校1200名学生中随机抽取100名学生进行知识测试（测试满分100分，得分均为整数），并根据这100人的测试成绩，制作了如下统计图表．100名学生知识测试成绩的频数表 成绩a（分） 频数（人） 50≤a＜60 10 60≤a＜70 15 70≤a＜80 m 80≤a＜90 40 90≤a≤100 15 由图表中给出的信息回答下列问题：（1）m= ____ ，并补全频数分布直方图；（2）小明在这次测试中成绩为85分，你认为85分一定是这100名学生知识测试成绩的中位数吗？请简要说明理由；（3）如果80分以上（包括80分）为优秀，请估计全校1200名学生中成绩优秀的人数．
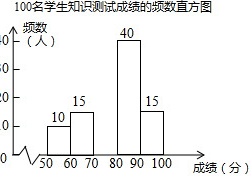今年5月15日，亚洲文明对话大会在北京开幕．为了增进学生对亚洲文化的了解，某学校开展了相关知识的宣传教育活动．为了解这次宣传活动的效果，学校从全校1200名学生中随机抽取100名学生进行知识测试（测试满分100分，得分均为整数），并根据这100人的测试成绩，制作了如下统计图表．100名学生知识测试成绩的频数表
| 成绩a（分） | 频数（人） |
| 50≤a＜60 | 10 |
| 60≤a＜70 | 15 |
| 70≤a＜80 | m |
| 80≤a＜90 | 40 |
| 90≤a≤100 | 15 |
（1）m= ____ ，并补全频数分布直方图；
（2）小明在这次测试中成绩为85分，你认为85分一定是这100名学生知识测试成绩的中位数吗？请简要说明理由；
（3）如果80分以上（包括80分）为优秀，请估计全校1200名学生中成绩优秀的人数．
题目解答
答案
解：（1）m=100-（10+15+40+15）=20，
补全图形如下：
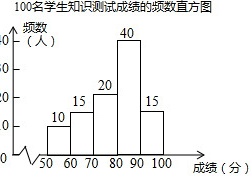
故答案为：20；
（2）不一定是，
理由：将100名学生知识测试成绩从小到大排列，第50、51名的成绩都在分数段80≤a＜90中，
但他们的中位数不一定是85分；
（3）估计全校1200名学生中成绩优秀的人数为1200×$\frac{40+15}{100}$=660（人）．
补全图形如下：
故答案为：20；
（2）不一定是，
理由：将100名学生知识测试成绩从小到大排列，第50、51名的成绩都在分数段80≤a＜90中，
但他们的中位数不一定是85分；
（3）估计全校1200名学生中成绩优秀的人数为1200×$\frac{40+15}{100}$=660（人）．
解析
步骤 1：计算m的值
根据频数表，m=100-（10+15+40+15）=20。
步骤 2：补全频数分布直方图
根据m的值，补全频数分布直方图。
步骤 3：判断85分是否为中位数
将100名学生知识测试成绩从小到大排列，第50、51名的成绩都在分数段80≤a＜90中，但他们的中位数不一定是85分。
步骤 4：估计全校1200名学生中成绩优秀的人数
根据频数表，80分以上（包括80分）的人数为40+15=55人，占总人数的$\frac{55}{100}$。因此，估计全校1200名学生中成绩优秀的人数为1200×$\frac{55}{100}$=660人。
根据频数表，m=100-（10+15+40+15）=20。
步骤 2：补全频数分布直方图
根据m的值，补全频数分布直方图。
步骤 3：判断85分是否为中位数
将100名学生知识测试成绩从小到大排列，第50、51名的成绩都在分数段80≤a＜90中，但他们的中位数不一定是85分。
步骤 4：估计全校1200名学生中成绩优秀的人数
根据频数表，80分以上（包括80分）的人数为40+15=55人，占总人数的$\frac{55}{100}$。因此，估计全校1200名学生中成绩优秀的人数为1200×$\frac{55}{100}$=660人。