题目
苯在内径为20 mm的圆形直管中作湍流流动,对流给热系数为 /((m)^2cdot K)-|||-如果流量和物性不变,改用内径为30 )mm的圆管,其对流给热系数将变为 () 。

题目解答
答案
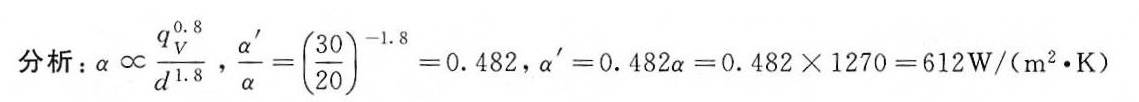
解析
考查要点:本题主要考查湍流条件下对流给热系数与管径的关系,需要结合流量不变时流速的变化规律,以及对流给热系数的经验公式进行推导。
解题核心思路:
- 流量不变时,流速与管径平方成反比;
- 对流给热系数在湍流中与雷诺数的0.8次方成正比;
- 雷诺数与管径成反比,结合上述关系推导出对流给热系数与管径的指数关系。
破题关键点:
- 建立流速与管径的关系:$v \propto \frac{1}{d^2}$;
- 将雷诺数代入努塞尔数公式,最终得到$\alpha \propto d^{-1.8}$;
- 利用比例关系计算新管径下的对流给热系数。
步骤1:分析流量与流速的关系
流量$Q$不变,管截面积$A = \frac{\pi d^2}{4}$,流速$v = \frac{Q}{A} \propto \frac{1}{d^2}$。
步骤2:关联对流给热系数与雷诺数
在湍流中,努塞尔数$Nu = 0.023 \cdot Re^{0.8} \cdot Pr^{0.4}$,其中$Re = \frac{v d}{\nu}$。
将$v \propto \frac{1}{d^2}$代入得$Re \propto \frac{1}{d}$,因此$Nu \propto Re^{0.8} \propto d^{-0.8}$。
步骤3:推导对流给热系数与管径的关系
由$Nu = \frac{\alpha d}{k}$得$\alpha = \frac{Nu k}{d} \propto d^{-0.8} \cdot d^{-1} = d^{-1.8}$。
步骤4:计算新管径下的对流给热系数
根据比例关系$\frac{\alpha'}{\alpha} = \left(\frac{d}{d'}\right)^{1.8}$,代入$d=20$ mm,$d'=30$ mm:
$\alpha' = 1270 \cdot \left(\frac{20}{30}\right)^{1.8} \approx 1270 \cdot 0.482 = 612 \, \text{W/(m}^2 \cdot \text{K)}.$